What size were the factions in the US election?
Tagged:MathInTheNews
/
Politics
/
R
/
Statistics
So we just had an election. You may have heard there were some rather sharply drawn sides. How big were each of the factions?
The Electoral College, barring mischief, will decide for Biden on 2020-Dec-14. Then on 2021-Jan-06, Congress must count the Electoral College ballots and certify the result. Again barring mischief, that will lead to a Biden presidential inauguration on Jan 20. In the meantime, let’s take a look at the popular vote, just to see the demographics who voted for whom, and who did not vote. Yes, even in the most important election since the American Civil War, a sizeable fraction of the population just… shrugged.
How many US voters are there, anyway?
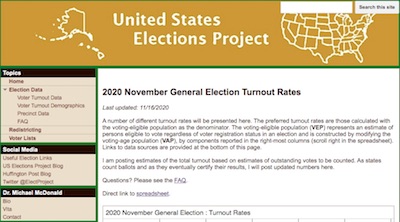 First, let’s turn to the US Elections Project to get an idea of how many votes were cast,
and how many were eligible to be cast. [1] The US Elections
Project is a non-partisan election data provider, led by Prof. Michael P. McDonald
of the PoliSci department at the University of Florida.
First, let’s turn to the US Elections Project to get an idea of how many votes were cast,
and how many were eligible to be cast. [1] The US Elections
Project is a non-partisan election data provider, led by Prof. Michael P. McDonald
of the PoliSci department at the University of Florida.
They start with the Voting Age Population (VAP), defined by the Bureau of the Census as everyone living in the US and older than 18 years. This is then modified to obtain the Voting Eligible Population (VEP) by subracting out non-citizens, felons or prisoners (depending on state law), and then apparently adding back in expatriate voters. This is as close an estimate as you’re likely to get, within the limits of social science, of how many people could vote in the US at any given time. [2]
McDonald gives us the following summary numbers, last updated 2020-Nov-16:
| Variable | Definition | Value |
|---|---|---|
| VAP | Voting age population | 257,605,088 |
| VEP | Voting eligible population | 239,347,182 |
| CAST | Votes actually cast | 159,555,940 |
That leads us to a point estimate of the probability that eligible folk will vote:
\[p \sim 159,555,940 / 239,247,182 = 0.6669\]… or the depressing equivalent that there is a 33.31% chance that an eligible voter will somehow fail to vote.
However, the above is just the maximum likelihood point estimate. Since $p$ is of course a random variable, it has some probability distribution. We’ll pull the same trick we’ve pulled several times now [3]: assume an uninformative uniform prior for $\Pr(p)$, and thus a Bayesian posterior distribution given $N$ eligible voters with $K$ actual voters, and a MAP estimator as the mode of that Beta distributions, and confidence limits:
\[\begin{align*} \Pr(p) & \sim \mathrm{Uniform}(0, 1) \\ \Pr(p | N, K) & \sim \mathrm{Beta}(K + 1, N - K + 1) \end{align*}\]So let’s see just how the posterior Beta distributions inform our uncertainty about the value of $p$:
> N <- 239247182 # VEP
> K <- 159555940 # Votes actually cast
> pmin <- 0.6665; pmax <- 0.6675 # Range where it's reasonably nonzero
> ps <- seq(from = pmin, to = pmax, length.out = 1000)
> prps <- dbeta(ps, shape1 = K + 1, shape2 = N - K + 1)
> pMAP <- ps[which.max(prps)]
> pCL <- quantile(rbeta(1000, shape1 = K + 1, shape2 = N - K + 1), probs = c(0.025, 0.975))
> source("~/Documents/laboratory/tools/graphics-tools.r")
> withPNG("./images/2020-11-30-who-voted.png", 600, 300, FALSE, function() { withPars(function() { plot(ps, prps, type = "l", lty = "solid", col = "blue", xlim = c(pmin, pmax), ylim = c(0, max(prps)), xlab = "p", ylab = "Density", main = "Posterior Beta Distribution: Probability of Voting"); abline(v = pMAP, lty = "dashed", col = "red"); abline(v = pCL, lty = "dashed", col = "black"); legend("topright", inset = 0.01, bg = "antiquewhite", legend = c(sprintf("Voting MAP: %.5f", pMAP), sprintf("95%% CL: %.5f - %.5f", pCL[[1]], pCL[[2]])), col = c("red", "black"), lty = "dashed", lwd = 2) }, pty = "m", bg = "transparent", ps = 16, mar = c(3, 3, 2, 1), mgp = c(1.7, 0.5, 0)) })
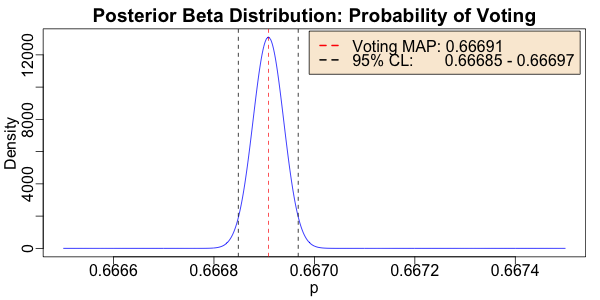 This tells us our best estimate of the probability of voting is 66.691%, and the 95%
confidence limit on that is 66.685% - 66.697%, which is a pretty narrow confidence limit.
(If you take hundreds of millions of measurements, you can beat the uncertainty down quite
a bit.)
This tells us our best estimate of the probability of voting is 66.691%, and the 95%
confidence limit on that is 66.685% - 66.697%, which is a pretty narrow confidence limit.
(If you take hundreds of millions of measurements, you can beat the uncertainty down quite
a bit.)
Also note that the simple-minded point estimate above, from dividing votes cast by VEP, was 66.69%, which is within a gnat’s whisker of this more nuanced Bayesian estimate. The rule is: if you start with an uniformative prior (here a prior uniform distribution), and have tons of data, then the Bayesian and maximum likelihood estimates converge very nicely. Bayesian methods give an advantage with smaller datasets for which you have informative priors, those priors being used to make up for the size of the dataset. On the other hand, your prior “knowledge” could also be prior “prejudice”; you don’t know which because it’s prior!
The unmistakeable bottom line is: no matter how skull-breakingly important this election was, about 1/3 of Americans eligible to vote didn’t seem to care. It’s an extremely interesting sociological question as to why: are they just too uninformed to know what voting means, or are they too discouraged by the abuses of the system to think their vote will count, or are they too poor/stressed/abused by employers to get time off to vote, or were they among the many victims of Republican voter suppression, or… It boggles the mind how dysfunctional we are!
… and how did they vote?
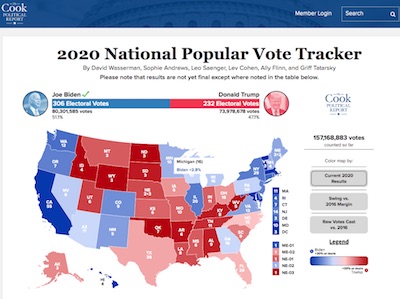 Now, the US Elections Project tells us whether people voted, but not how. For that,
we turn to the Cook Political Report’s 2020 National Popular Vote
Tracker. [4]
Now, the US Elections Project tells us whether people voted, but not how. For that,
we turn to the Cook Political Report’s 2020 National Popular Vote
Tracker. [4]
Considering only the presidential election, they report the following breakdown of votes cast:
| Candidate | Votes | Percent |
|---|---|---|
| Biden | 80,301,585 | 51.09% |
| Trump | 73,978,678 | 47.07% |
| Other | 2,888,620 | 1.84% |
| Total | 157,168,883 | 100.00% |
So, yeah: Biden wins with a margin of about 4% of the votes cast, and about 1.8% of the votes were jokers who voted 3rd party. (Which, in a first past the post system with 2 dominant parties, like the US, is stupid. Unless, of course, you are one of the few fortunates to live in states with ranked-choice voting, in which case congratulations.)
But… it gets a bit darker and weirder when we consider percentages not of the votes cast, but of the eligible votes, i.e., the VEP. Now Cook Political Report shows a total of 157,168,883 votes cast while the US Elections Project is 159,555,940 or a bit over 2 million more votes. We’ll chalk that up to slight differences in reporting dates.
Which do we use? I’m tempted to use the Cook data, to stay within a dataset. But let’s use the higher number from US Elections Project, to be more generous about assuming people voted. It’s slightly more optimisitic. In that case, the number of non-voters is:
NonVoters = VEP - VotesCast = 239,247,182 - 159,555,940 = 79,691,242
So here’s the breakdown of candidates, including not voting as a “candidate”, using as our percentage denomiator VEP = 239,247,182:
| Candidate | Votes | Percent of VEP | |
|---|---|---|---|
| Biden | 80,301,585 | 33.56% | |
| Trump | 73,978,678 | 30.92% | |
| Other | 2,888,620 | 1.21% | |
| NonVoter | 79,691,242 | 33.31% |
(Percentages don’t quite add up to 100% because we’ve mixed counts from 2 datasets.)
The somewhat dispiriting result is that the non-voters comprised almost the largest faction, statistically indistinguishable from Biden and barely distinguishable from Trump. (The third party voters are still just irritating.)
The bottom line
We are divided into roughly 3 factions: Democrats, Republicans, and eligible non-voters. We desperately need to figure out the various reasons for not voting, and mend that problem. This includes:
- breaking the stranglehold of gerrymandering (perhaps Brin’s geometric compactness/minimum overlap for districts [5]),
- making voting a couple days long,
- making at least one of those days a national holiday,
- mandating time off from work to vote,
- restoring polling places closed in poor districts,
- striking back really hard against Republican voter suppression,
… and oh so many things.
We have a lot of work to do.
Notes & References
1: M McDonald, “2020 November General Election Turnout Rates”, United States Elections Project, accessed 2020-Nov-30, last update 2020-Nov-16. ↩
2: The FAQ on the US Elections Project page has much more detail about how this is done. ↩
3: See 4 previous posts on estimating a binomial response probability using a uniform prior and a Beta posterior:
- “Is the racial makeup of the Boston Police Department unrepresentative?”,
- “Election Night of the Living Beta Binomials”,
- “Pfizer/BioNTech vaccine interim readout: 90% efficacy!”, and
- “Moderna/Lonza vaccine interim readout: 95% efficacy!” ↩
4: Cook Political Report, “2020 National Popular Vote Tracker”, downloaded 2020-Nov-30.↩
5: D Brin, “The ‘Minimal Overlap’ Solution to Gerrymandered Injustice”, Medium.com, 2017-Sep-23. ↩
Gestae Commentaria
Comments for this post are closed pending repair of the comment system, but the Email/Twitter/Mastodon icons at page-top always work.