Updated Update: Ukrainian Estimates of Russian Casualties

We’ve (again) updated our estimate of when Russian casualties will reach 200k, according to the Ukrainian Ministry of Defence’s published data. This time with an improved (though not perfect) prediction method.

Ukrainian Ministry of Defence and Russian Casualty Counts

Background: the Ukrainian Ministry of Defence publishes daily estimates of various sorts of Russian casualties. Cursory investigation shows they are higher than the OSInt numbers from Oryx (where they demand documentation of everything, a high standard in war) but lower than other media sources. So… not really verifiable, but not the most extreme numbers, either.

We’ve previously written ^{[1] [2]} about collecting these data, looking at odd time patterns in cruise missile attacks that probably say something about Russian supply chains, and building regression models to project future casualty numbers.

Today, 2023-May-09, was the upper confidence limit on the date we thought Russian losses of soldiers would reach 200,000. Let’s check in to see what’s going on.

Data and Methods

We’ve updated the data as of today’s report (2023-May-09), and updated the R script to do a slightly better prediction of 200k day; all are available here for peer review. ^[3] As previously observed, the 2023-Apr-30 data is missing.

Results

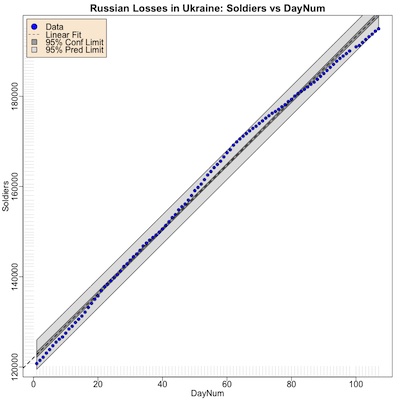For the most part, things look pretty similar to the way they looked last time, with just a continuation of trends.

Shown here, for example, is the trend of number of Russian soldiers killed (as counted by the UKR MoD, of course) versus the day number since 2023-Jan-22. It’s pretty much a continuation of the trend, with quite tight confidence intervals and prediction intervals. The fact that a linear model fits well is a bit surprising, perhaps indicative of a relatively constant, grinding level of war.

The fit is indeed excellent:

Coefficients:
             Estimate Std. Error t value Pr(>|t|)    
(Intercept) 1.220e+05  3.149e+02   387.5   <2e-16 ***
x           7.123e+02  5.099e+00   139.7   <2e-16 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 1613 on 104 degrees of freedom
Multiple R-squared:  0.9947,	Adjusted R-squared:  0.9946 
F-statistic: 1.951e+04 on 1 and 104 DF,  p-value: < 2.2e-16

One feature of the plot above possibly worth noting is that the data points appear to bend downward, with a slower death rate on about day 60. The linear fit is approximately an average of the previous high slope and the new lower slope. That means any prediction here will include influence from the early high slope, and hence underestimate time time to 200k dead.

Indeed, that’s what we observe: we were sure today would be The Very Bad Day, but it is not. Today’s figure was 195,620.

We could, of course, implement a nonlinear model to address this. E.g., a piecewise linear model with a hinge at day 60 would do the trick, or we could actually let the hinge date be a fit parameter. That would lead to a 4-parameter model: 2 slopes, 2 intercepts, 1 hinge date, but 1 constraint that the lines meet exactly at the hinge date.

However, that would be a more complex model, rather ill-motivated by anything other than a desire to fit the data better when we already have an excellent fit. So let’s just live with the caution that our estimates will be underestimates, and move on.

Now on to predictions!

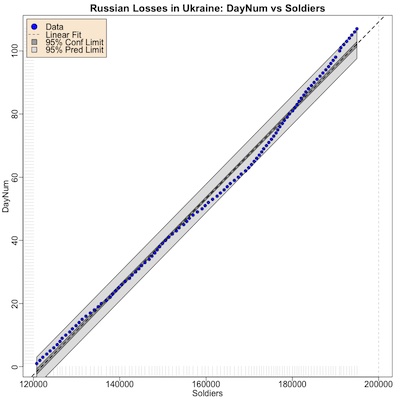
Last time, we used the regression model of Soldiers as a function of DayNum, and back-solved to find the date when the number of casualties was about 200k. That’s… awkward, especially since the 95% confidence intervals don’t work linearly like that.

So this time we’ll regress DayNum on Soldiers, and use the number of losses at 200k to directly predict the day number and its 95% confidence limit. The fit is shown here. (Don’t spend too much time staring at it, since it’s just the transpose of the fit above.)

The vertical dashed gray line is 200k soldiers lost. As you can see, things are not yet that bad.

The fit is, of course, equally as excellent as the fit above:

Coefficients:
              Estimate Std. Error t value Pr(>|t|)    
(Intercept) -1.701e+02  1.617e+00  -105.2   <2e-16 ***
Soldiers     1.396e-03  9.998e-06   139.7   <2e-16 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 2.258 on 104 degrees of freedom
Multiple R-squared:  0.9947,	Adjusted R-squared:  0.9946 
F-statistic: 1.951e+04 on 1 and 104 DF,  p-value: < 2.2e-16

When we use the linear model predictor to guess when casualties reach 200k, and what the 95% lower and upper confidence limits are, we get:

         fit        lwr        upr
1 2023-05-11 2023-05-06 2023-05-15

Three things are worth noting here:

1. The most likely date, using data up through today, is 2023-May-11. For the reasons discussed above, the bend in slope at day 60 means this is probably a slight underestimate and the real event will be a little bit after that.
2. The 95% confidence limit is from 2023-May-06 to 2023-May-15. So any time from May 11 to May 15 is probably a decent estimate to use.
3. The lower confidence limit, 2023-May-06, is in the past. We know with 100% confidence that the date will be in the future, so this is nonsense! We’re using an acausal (unaware of time and cause) linear model to predict a causal (time series, where things happen in a certain order) to predict. This is, at some level, wrong. Probably if I were to take this seriously, I should go get out my old copy of Box, Jenkins, and Reinsel ^[4] (or even something more modern like Hyndman and Athanasopoulos ^[5]) and read about time series forecasting. Both of them are sitting on my shelf, but Vīta brevis, ars longa, occāsiō praeceps, experīmentum perīculōsum, iūdicium difficile, as Hippocrates is supposed to have said (ok, in Greek, but I only know it in Latin).

The Weekend Conclusion

Using slightly (though not completely) better methods, we estimate 200k Russian casualties sometime in 2023-May-11 to 2023-May-15. These dates are likely (slight) underestimates, i.e., the true date will likely be a bit later.

Notes & References

1: Weekend Editor, “Do the Ukrainian Reports of Russian Casualties Make Sense?”, Some Weekend Reading blog, 2023-Apr-15. ↩

2: Weekend Editor, “Update: Ukrainian Estimates of Russian Casualties”, Some Weekend Reading blog, 2023-May-01. ↩

3: Weekend Editor, “Updated R script to analyze Ukrainian reports of Russian casualties”, Some Weekend Reading blog, 2023-May-09.

There is also a textual transcript of running this, so you can check that it says what I told you.

We’ve also archived a .zip file of the original images uploaded by the Ukrainian MoD, and a .tsv format spreadsheet we constructed from that for analysis.

NB: There are also some subroutine files for graphics and analysis pipeline building (graphics-tools.r and pipeline-tools.r) that are loaded from our private repository. If you want those too for reproduction purposes, drop us an email and we’d be happy to send them along to you.

You might have to rename the script, create a data directory, and put the .tsv file in it with the appropriate name to make this work. Ask if there’s a problem. Here at Château Weekend, we are peer-review-friendly. ↩

4: G Box, et al., “Time Series Analysis: Forecasting and Control (5th ed)”, Wiley, 2015. Mine is the older 3rd edition of 1994. ↩

5: R Hyndman & G Athanasopoulos, “Forecasting: Principles and Practice”, Open Access Textbooks, 2018. ↩