Update: Ukrainian Estimates of Russian Casualties

We’ve updated our estimate of when Russian casualties will reach 200k, according to the Ukrainian Ministry of Defence’s published data.

Updated what?

The Ukrainian Ministry of Defence has been making daily reports of their estimates of Russian casualties in the We previously blogged about this, collecting about 90 days worth of data and building regression models and biclustering the correlation matrix.

We’ve now updated the dataset with another couple weeks of data. It now covers 101 consecutive calendar days (2023-Jan-22 to 2023-May-02). There is 1 missing data point (2023-Apr-30).

Estimated date of 200k Russian casualties

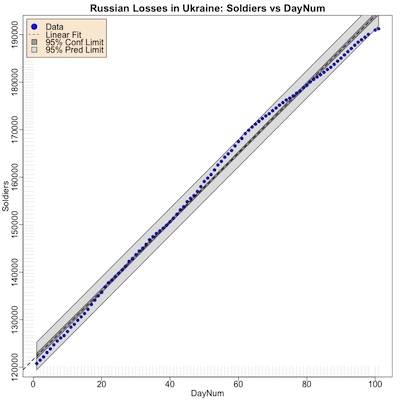We built lots of regression models, really just fishing around rather than hypothesis testing. But in particular, one model was number of soldiers lost vs time:

… along with numerous other models of casualty statistics vs time and versus each other. The data was highly self-correlated and oddly smooth.

The count of Russian soldiers lost, shown here, is very well fit by a linear model. It does appear, beginning about day 60, there was a slight decrease in slope. But overall the fit is almost suspiciously excellent.

The regression was, in fact, almost bizarrely statistically significant and highly predictive, with $R^2 \sim 99.54\%$:

Residuals:
    Min      1Q  Median      3Q     Max 
-3505.9 -1207.5    66.0   932.3  2656.0 

Coefficients:
             Estimate Std. Error t value Pr(>|t|)    
(Intercept) 1.216e+05  2.893e+02   420.4   <2e-16 ***
x           7.239e+02  4.971e+00   145.6   <2e-16 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 1437 on 98 degrees of freedom
Multiple R-squared:  0.9954,	Adjusted R-squared:  0.9954 
F-statistic: 2.121e+04 on 1 and 98 DF,  p-value: < 2.2e-16

Today we used this updated model to predict when Russian casualties would break 200k. We first get an estimate by using the model predictions vs time, subtracting 200,000 and looking for the time when that happens with the usual root finder:

> uniroot(function(dn) { predict(mdl7, newdata = data.frame("x" = dn)) - 200000 }, interval = c(100, 150))
$root
[1] 108.2582

$f.root
1 
0 

$iter
[1] 1

$init.it
[1] NA

$estim.prec
[1] 41.74184

That suggests where to look, so let’s assemble a more human-readable table of date, mean estimated number of casualties, and the 95% lower and upper confidence limits:

> foo <- data.frame(DayNum = 100:110, Date = as.Date("2023-01-22") + 99:109, predict(mdl7, newdata = data.frame(x = 105:115), interval = "prediction")); colnames(foo)[3:5] <- c("Soldiers", "LCL", "UCL"); foo
   DayNum       Date Soldiers      LCL      UCL
1     100 2023-05-01 197641.4 194726.3 200556.5
2     101 2023-05-02 198365.3 195448.4 201282.3
3     102 2023-05-03 199089.2 196170.4 202008.0
4     103 2023-05-04 199813.1 196892.4 202733.8
5     104 2023-05-05 200537.0 197614.4 203459.7
6     105 2023-05-06 201260.9 198336.3 204185.5
7     106 2023-05-07 201984.8 199058.2 204911.4
8     107 2023-05-08 202708.7 199780.1 205637.3
9     108 2023-05-09 203432.6 200501.9 206363.3
10    109 2023-05-10 204156.5 201223.7 207089.3
11    110 2023-05-11 204880.4 201945.5 207815.3

Results:

1. We estimate the number of Russians killed, admittedly according to the Ukrainian Ministry of Defence, will reach 200k on or about 2023-May-05. The previous estimate, using data through 2023-Apr-15, was for 2023-May-07, so there are slightly more deaths than previously expected.
2. The 95% confidence limit on the number of casualties on that day is 197614 - 203459 (but ignore the spurious number of significant figures; basically plus or minus about 3k).
3. If you want to be 97.5% sure the Russian casualties will exceed 200k, then the date for that is 2023-May-09.

The Weekend Conclusion

In most ways that will be a sad day for the entire world, as has been the entire affair of the invasion of Ukraine. On the other hand, perhaps for Ukraine it will be a glimmer of hope of repelling the invaders.

Notes & References

1: Nope. Read the previous post about Russian casualties for references.