Springtime for Shutdowns II: A Bayesian Coda

A little Bayesian coda on confidence limits for the probability of a government shutdown, given a Republican house.

A Bayesian Coda

Previously, we wrote about the strong association between US government shutdowns and Republican control of the House. Today, we’ll add a little Bayesian coda.

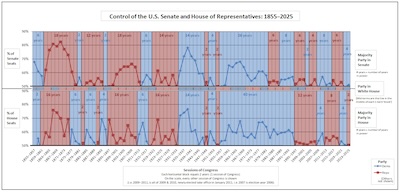We’d previously looked at data going back 30 years, to the ascent of the rather nihilistic Republicans of the modern sort, in the personage of Newt Gingrich as speaker. Looking at party divisions of the US congress over those years, we see there were 15 congressional terms (2 years each), of which 11 were Republican and 6 were Democratic.

We also observe 6 shutdowns, all Republican. (We’re counting this term, because (a) there was a technical shutdown last weekend, though quickly fixed, and (b) the term isn’t over yet and the “Freedom Caucus” is quite determined and still has time to throw Molotov cocktails at the federal government.)

So that leads to point estimates of the probability of a shutdown given House partisanship:

\[\begin{align*} \Pr(\mbox{Shutdown} | \mbox{House Republican}) &= \frac{6}{11} = 54.5\% \\ \Pr(\mbox{Shutdown} | \mbox{House Democratic}) &= \:\:\frac{0}{6} = \:\:0.0\% \end{align*}\]

That’s… fine, as far as it goes. Depressing, but that’s life.

How can we improve this? It turns out we can use Bayes Rule to get a posterior distribution for the probabilities above, and the width of that distribution is our uncertainty.

We’ve worked through the details many times on this Crummy Little Blog That Nobody Reads (CLBTNR), the first time being when we were thinking about the uncertainty on vaccine efficacy ratios.

The basic idea is that the count of shutdowns is binomially distributed, with some probability of shutdown parameter $p$. Using Bayes Rule, we can infer that $p$ is distributed according to a Beta distribution: \(p \sim \mbox{Beta}(k + 1, N - k + 1)\) when we see $N$ terms of congress over which there were $k$ shutdowns.

\[\begin{align*} p_{\mbox{Shutdown} | \mbox{House Republican}} &\sim \mbox{Beta}(6 + 1, 11 - 6 + 1) \\ p_{\mbox{Shutdown} | \mbox{House Democratic}} &\sim \mbox{Beta}(0 + 1, \:\:6 - 0 + 1) \end{align*}\]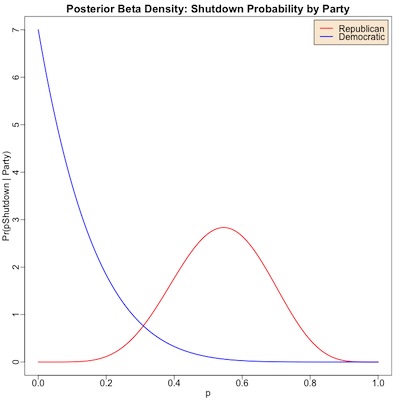

Let’s consider what shape those distributions have! After a few quick revisions to the R script we wrote for the previous post, and we get the plot shown here.

• The red curve is for when Republicans control the House. It is the distribution for $p$, the probability of a shutdown under their control, inferred from the data.
  • The point estimate above was 54.5%, and that’s where the red curve peaks.
  • The width of the red curve gives us some idea about confidence limits. Using the Beta quantile function, the 95% confidence limits say we’re pretty sure $p$ is in [0.276, 0.789].
• The blue curve is for when the Democrats control the House. It is also the distribution for $p$, the probability of a shutdown under their control, inferred from the data.
  • The point estimate above was 0%, and indeed that’s where the blue curve peaks.
  • The shape of the blue curve tells us we’re pretty sure $p$ is in [0.003, 0.409].

Basically, the red and blue curves show us that, even when we take into account uncertainty from the only 15 terms of data, we’re quite sure Republicans just make more trouble with shutdowns.

It’s their brand.

The Weekend Conclusion

Republican control of the House is at the root of every US federal government shutdown for more than a generation. The statistical data is clear; when will the political consensus against Republicans also be clear?

(Ceterum censeo, Trump incarcerandam esse.)

---

Notes & References

Nope.