On the ratio of Beta-distributed random variables

[Warning: Post contains full frontal nerdity. Bug reports appreciated!] I finally got a copy of Pham-Gia’s paper on the distribution of the ratio of 2 independent Beta-distributed random variables. While I still have some childhood trauma around hypergeometric functions like ${}_{2}F_{1}()$ and its even scarier big brother ${}_{3}F_{2}()$… it’s time to face my fears.

The three B’s: Bernoulli, Binomial, and Beta

Suppose you flip a loaded coin that has probability $p$ of coming up heads. That’s a Bernoulli distribution, with just 2 discrete values:

\[\left\{ \begin{align*} \Pr\left(\mbox{heads}\right) &= p \\ \Pr\left(\mbox{tails}\right) &= 1 - p \end{align*} \right.\]

Now suppose you do that $N$ times, and observe that heads comes up $k$ times. That’s a binomial distribution:

\[\Pr(k | N, p) = \binom{N}{k} p^k (1-p)^{(N-k)}\]

Next, suppose you don’t know how much the coin is loaded. Somebody lets you take $N$ flips, and you observe $k$ heads.

What should you believe about $p$, the probability the coin comes up heads? A naïve estimate would just give the single point value $p = k/N$. A better approach is to regard $p$ as a random variable, whose distribution you’re inferring from experiment. The Bayesian way to do this is to start with a prior distribution that summarizes your knowledge before the experiment. If you don’t know anything, then it’s hard to beat a uniform distribution on $[0, 1]$. This can conveniently be done with the Beta distribution of the first kind:

\[\Pr(p | \alpha, \beta) = \frac{p^{\alpha - 1} (1 - p)^{\beta - 1}}{B(\alpha, \beta)}\]

where the normalization is $B(\alpha, \beta)$ is the complete Beta function.

It’s pretty clear that the uniform distribution is $\alpha = 1, \beta = 1$.

At that point it’s a pretty straightforward application of Bayes Rule to show that the posterior distribution for $p$ will be Beta-distributed with parameters $\alpha = k + 1$ (successes + 1), and $\beta = N - k + 1$ (failures + 1). So all you have to do is count the number of trials and successes to get a posterior probability distribution that completely reflects your knowledge (and uncertainty!) of $p$.

Why we’re interested: vaccine efficacy confidence intervals

The reason we’re interested in this is vaccine efficacy confidence intervals. (Hey, COVID-19 pandemic, right?) Basically you have $N_v$ people enrolled in the vaccine arm of the trial, and see $I_v$ infections. At the same time, you have $N_c$ people enrolled in the control arm, and observe $I_c$ infections.

The coin we flipped above is here: heads you get the disease, tails you don’t. We’d like to know how much the vaccine lowers your risk of disease.

So point estimates of the probability of infection in each arm are:

\[\begin{align*} p_v &= I_v / N_v \\ p_c &= I_c / N_c \end{align*}\]

(We’d of course like to use a posterior Beta distribution instead of a point estimate here.)

Then the vaccine efficacy $E$ is how much the risk is lowered, compared to the unvaccinated control arm:

\[E = 100\% \times \frac{p_c - p_v}{p_c} = 100\% \times \left(1 - \frac{p_v}{p_c}\right)\]

Now if we believe that $p_v$ and $p_c$ are Beta-distributed, then given the clinical trial as a bunch of disease-catching coin flips, the vaccine efficacy is distributed as (a trivial linear function of) the ratio of a couple of independent Beta variables.

Ok, so what’s the distribution of a ratio of independent Beta variables? There are a variety of ways to approach this, and we’ll compare several of them in an upcoming post. For now, we’re going to fight our way through a paper which gives the exact Bayesian result.

Exact solution: the probability distribution function (PDF) of a ratio of 2 Beta-distributed random variables

We’ll look specifically at the application of all this to the case of vaccine efficacies in a later post. For now, let’s just examine the mathematical question of what the distribution is for the ratio of two Beta-distributed variables. The exact solution was published in 2000 by Pham-Gia. ^[1] It lives behind an execrable paywall, and was thus devilishly difficult to acquire without paying ransom. Fortunately, I know people who know people who know people; somebody or other in that chain found it or had institutional access, and passed it back up the chain. Whoever you are, my thanks.

The problem

Consider 2 Beta-distributed variables $p_1$ and $p_2$:

\[\begin{align*} \Pr(p_1) &= \frac{p_{1}^{\alpha_{1}-1}(1-p_{1})^{\beta_{1}-1}}{B(\alpha_1, \beta_1)} \\ \Pr(p_2) &= \frac{p_{2}^{\alpha_{2}-1}(1-p_{2})^{\beta_{2}-1}}{B(\alpha_2, \beta_2)} \end{align*}\]

We then ask: if we compute their ratio $R = p_1 / p_2$, then what are the PDF & CDF of $\Pr(R)$? Ifwe knew the answer, particularly the CDF (or even better the quantile function, which is the functional inverse of the CDF!), we could calculate 95% confidence intervals on the ratio.

Ranges

It’s important to understand the ranges of each of the variables $p_1$, $p_2$, and $R$ so that as we transform variables we don’t accidentaly step outside reality. This will help us keep the integration limits straight. Because $p_1$ and $p_2$ are from the standard Beta distribution, we have:

\[0 \le p_1, p_2 \le 1\]

(Usually these are proportions or probabilities, so we certainly want to stay in $[0, 1]$!)

$R$, on the other hand, is a bit more gnarly. Since both $p_1$ and $p_2$ are non-negative, then surely $R$ is also non-negative, i.e., 0 is a lower bound. But the denominator $p_2$ can of course be arbitrarily near 0, so if at the same time the numerator $p_1$ is finite (stepping carefully around the land mine at 0/0), then the upper bound must be infinite:

\[0 \le R \le +\infty\]

(Values of $R \gt 1$ will, when we apply this to vaccine efficacies, result in negative efficacies. Is that meaningful? Yes: your vaccine could make things worse, making the vaccinees more susceptible to disease… which is surely negative efficacy, no?)

Changes of variables

Our strategy is to start with the joint density $\Pr(p_1, p_2)$ and then do various tortured changes of variables to eliminate one of $p_1$ or $p_2$ in favor of $R$, and express the residual integral in terms of a hypergeometric function ${}_{2}F_{1}()$.

How complicated can it be? Well, there’s lots of detail coming up, but really it comes down to the fact that with 3 variables $p_1, p_2, R$ there are only 2 ways to eliminate one of them in favor of $R$. Either we substitute out $p_1$ in favor of $p_2, R$ via:

\[\begin{align*} p_1 &= p_2\, R \\ dp_1 &= p_2\, dR \end{align*}\]

This is appropriate for $0 \le R \le 1$, since if $R \gg 1$ it could force a value of $p_1 > 1$, which takes us out of its allowed range.

Or we substitute out $p_2$ in favor of $p_1, R$ via:

\[\begin{align*} p_2 & = \frac{p_1}{R} \\ dp_2 &= -\frac{p_1}{R^2} dR \end{align*}\]

This is correspondingly appropriate for $1 \lt R$, as it guarantees $p_2 \le 1$, as the range requires. (We’ll eventually lose the minus sign, either taking absolute value of Jacobians, or more reasonably, keeping careful track of the limits of integeration and swapping them when appropriate to cancel a minus sign.)

So we’ll need to do both transformations, piecewise over the range of $R$.

Double the workload. Le sigh… who coulda seen that coming?

Reading off the distribution of $R$

I like to do these changes of variable by looking at the normalization integral for the joint distribution. That way, as you change variables, the integration measure will force you to pick up the Jacobian properly. The joint distribution of $p_1$ and $p_2$ is, since they’re assumed independent, just the product of their individual distributions. So the normalization integral is pretty straightforward to write down:

\[1 = \frac{1}{B(\alpha_1, \beta_1) B(\alpha_2, \beta_2)} \int_0^1\!\!\!\!dp_1 \int_0^1\!\!\!\!dp_2\, p_1^{\alpha_1 - 1} (1-p_2)^{\beta_1 - 1} p_2^{\alpha_2 - 1} (1-p_2)^{\beta_2 - 1}\]

Next, we’ll use both the transformations above to get the integral in 2 pieces, one using $(p_2, R)$ and another using $(p_1, R)$. The first will involve an integral over $R$ from 0 to 1, while the second will integrate from 1 to $+\infty$. Then we’ll do a little razzle-dazzle high school algebra to pull the $R$ integrations to the left, and thus be able to read off the distribution of $R$. It’ll be a piecewise function, with one piece for $0 \le R \le 1$ and another for $R \gt 1$:

\[\begin{alignat*}{4} 1 & = \frac{1}{B(\alpha_1, \beta_1) B(\alpha_2, \beta_2)} && \left[ \int_0^1\!\!\!\!dp_2 \int_0^1\!\!\!\!dR\, p_2 (Rp_2)^{\alpha_1 - 1} (1 - Rp_2)^{\beta_1 - 1} p_2^{\alpha_2 - 1} (1-p_2)^{\beta_2 - 1} \right. \\ & && \left. + \int_0^1\!\!\!\!dp_1 \int_1^{+\infty}\!\!\!\!\!\!\!\!dR\, \frac{p_1}{R^2} p_1^{\alpha_1 - 1} (1-p_1)^{\beta_1 - 1} \left(\frac{p_1}{R}\right)^{\alpha_2 - 1} \left(1 - \frac{p_1}{R}\right)^{\beta_2 - 1}\right] \\ & = \frac{1}{B(\alpha_1, \beta_1) B(\alpha_2, \beta_2)} && \left[ \int_0^1\!\!\!\!dR\, R^{\alpha_1 - 1} \int_0^1\!\!\!\!dp_2\, p_2^{\alpha_1 + \alpha2 - 1} (1-p_2)^{\beta_2 - 1} (1-Rp_2)^{\beta_1 - 1} \right. \\ & && \left. + \int_1^{+\infty}\!\!\!\!\!\!\!\!dR\, \frac{1}{R^{\alpha_2 + 1}} \int_0^1\!\!\!\!dp_1\, p_1^{\alpha_1 + \alpha_2 -1} (1-p_1)^{\beta_1 - 1} \left(1 - \frac{p_1}{R}\right)^{\beta_2 - 1}\right] \end{alignat*}\]

From this we can directly read off the PDF for $R$, piecewise for $0 \le R \le 1$ and similarly for $R \gt 1$, respectively from each of the 2 terms:

\[\left\{ \begin{alignat*}{6} \Pr(R | 0 \le R \le 1) &= \frac{1}{B(\alpha_1, \beta_1) B(\alpha_2, \beta_2)} & \cdot & R^{\alpha_1 - 1} & \cdot & \int_0^1\!\!\!\!dp_2\, p_2^{\alpha_1 + \alpha2 - 1} (1-p_2)^{\beta_2 - 1} (1-Rp_2)^{\beta_1 - 1} \\ \Pr(R | R \gt 1) &= \frac{1}{B(\alpha_1, \beta_1) B(\alpha_2, \beta_2)} & \cdot & \frac{1}{R^{\alpha_2 + 1}} & \cdot & \int_0^1\!\!\!\!dp_1\, p_1^{\alpha_1 + \alpha_2 -1} (1-p_1)^{\beta_1 - 1} \left(1 - \frac{p_1}{R}\right)^{\beta_2 - 1} \end{alignat*} \right.\]

These still contain a residual $p$-integral each, but we’ll see next how to interpret those in terms of the hypergeometric function ${}_{2}F_{1}()$ with various tortured arguments.

Hypergeometric functions

Ok, so what’s this hypergeometric thingummy I’ve been mumbling about? I approach this subject with some caution, due to some childhood trauma around hypergeometric functions. ^[2]

Hypergeometric functions got their start in the 1600s, but hit it big in the 1800s with major players like Euler, Gauss, Riemann, and Kummer coming up for bat. They’re at once mind-numbingly complex (at least to me, since they’re kind of my kryptonite) with a bajillion special cases, and amazingly versatile. You can express almost all the special functions of theortical physics (Bessel functions and the like) in terms of hypergeometric functions.

So there’s a temptation: if you can just learn everything about hypergeometric functions, you can master nearly all of 19th century physics. The bug, of course, is that nobody can master all of the lore of hypergeometric functions. Least of all me!

Like most magical artifacts, they are best approached by wizards and avoided by mundanes. I am not a wizard in these matters, and thus approach with some fear and considerable respect for the virtue of keeping one’s fingers out of the gears.

As a matter of definition, in the unit disk $|z| \lt 1$ in the complex plane, the hypergeometric function of interest at the moment is defined by a power series (and by analytic continuation outside the disk, stepping carefully around the branch points at 1 and infinity):

\[{}_2F_1(a, b; c; z) = \sum_{n=0}^{+\infty} \frac{(a)_n (b)_n}{(c)_n} \frac{z^n}{n!} = 1 + \frac{ab}{c} \frac{z}{1!} + \frac{a(a+1)b(b+1)}{c(c+1)} \frac{z^2}{2!} + \cdots\]

If $c$ is a non-positive integer, it’s undefined or infinite. The funny parenthetical dingus is the rising Pochammer symbol:

\[(q)_n = \left\{ \begin{array}{ll} 1 & n = 0 \\ q(q+1)\cdots(q+n-1) & n \gt 0 \end{array} \right. = \frac{\Gamma(q+n)}{\Gamma(q)}\]

An interesting special case for us will be when $a$ or $b$ are nonpositive integers (as with counts in a clinical trial), in which case the Pochammer symbols eventually include a 0 and the series thus terminates, resulting a polynomial. True, it will be a polynomial of very high order (say 15,000 participants in a trial arm), but a polynomial nonetheless!

That’s all… fine, if you like that sort of thing. But what does it have to do with the integrals we have to do above? Well, it turns out that ${}_{2}F_{1}()$ has an integral representation, as well, apparently due to Euler:

\[{}_2F_1(a,b;c;x) = \frac{1}{B(a, c-a)} \int_0^1\!\!\!\!du\, u^{a-1} (1-u)^{c-a-1} (1-xu)^{-b}\]

This is the trick that Pham-Gia used to get the density distribution in closed form (at least, if you regard ${}_{2}F_{1}()$ as “closed”…), by recognizing the integrals above as special cases of this.

Expressing the residual $p$-integrals in hypergeometric terms

Basically we take the above equations for $\Pr(R)$ with residual integrals , and recognize that the annoying integral in them can, with a suitable change of variables, be made identical to the integral representation of ${}_{2}F_{1}()$.

Case $0 \le R \le 1$:

The dictionary of variables to recognize the hypergeometric integral is:

\[\begin{align*} u &= p_2 \\ a &= \alpha_1 + \alpha_2 \\ b &= 1 - \beta_1 \\ c &= \alpha_1 + \alpha_2 + \beta_2 \end{align*}\]

That gives the final result for small $R$ of:

\[\Pr(R | 0 \le R \le 1) = \frac{B(\alpha_1 + \alpha_2, \beta_2)}{B(\alpha_1, \beta_1) B(\alpha_2, \beta_2)} R^{\alpha_1 - 1} {}_2F_1(\alpha_1 + \alpha_2, 1 - \beta_1; \alpha_1 + \alpha_2 + \beta_2; R)\]

And that’s Pham-Gia’s first result on p. 2698.

Case $1 \le R$:

Here the dictionary is slightly different:

\[\begin{align*} u &= p_1 \\ a &= \alpha_1 + \alpha_2 \\ b &= 1 - \beta_2 \\ c &= \alpha_1 + \alpha_2 + \beta_1 \end{align*}\]

That gives the final result for large $R$ of:

\[\Pr(R | 1 \lt R) = \frac{B(\alpha_1 + \alpha_2, \beta_1)}{B(\alpha_1, \beta_1) B(\alpha_2, \beta_2)} \frac{1}{R^{\alpha_2 + 1}} {}_2F_1(\alpha_1 + \alpha_2, 1 - \beta_2; \alpha_1 + \alpha_2 + \beta_1; 1/R)\]

And that’s Pham-Gia’s second result on p. 2699.

To summarize the PDF result:

\[\left\{ \begin{alignat*}{6} \Pr(R | 0 \le R \le 1) &= \frac{B(\alpha_1 + \alpha_2, \beta_2)}{B(\alpha_1, \beta_1) B(\alpha_2, \beta_2)} &\cdot& R^{\alpha_1 - 1} &\cdot& {}_2F_1(\alpha_1 + \alpha_2, 1 - \beta_1; \alpha_1 + \alpha_2 + \beta_2; R) \\ \Pr(R | 1 \lt R) &= \frac{B(\alpha_1 + \alpha_2, \beta_1)}{B(\alpha_1, \beta_1) B(\alpha_2, \beta_2)} &\cdot& \frac{1}{R^{\alpha_2 + 1}} &\cdot& {}_2F_1(\alpha_1 + \alpha_2, 1 - \beta_2; \alpha_1 + \alpha_2 + \beta_1; 1/R) \end{alignat*} \right.\]

Moments of the ratio, including the mean

We can also directly calculate the moments of $R$ (where the 1st moment is of course the familiar mean). We do this not by heroic integration against the distribution above, but from the properties of the Beta-distributed $p_1, p_2$ that go into the ratio $R$.
Because $p_1$ and $p_2$ are statistically independent, the moment integral factors into 2 separate pieces:

\[\begin{align*} E\left[R^k\right] & = \int_0^1\!\!\!\!dp_1 \int_0^1\!\!\!\!dp_2 \left(\frac{p_1}{p_2}\right)^k \frac{p_1^{\alpha_1 - 1}(1-p_1)^{\beta_1 - 1}}{B(\alpha_1, \beta_1)} \cdot \frac{p_2^{\alpha_2 - 1}(1-p_2)^{\beta_2 - 1}}{B(\alpha_2, \beta_2)} \\ & = \int_0^1\!\!\!\!dp_1 p_1^k \frac{p_1^{\alpha_1 - 1}(1-p_1)^{\beta_1 - 1}}{B(\alpha_1, \beta_1)} \cdot \int_0^1\!\!\!\!dp_2 \frac{1}{p_2^k} \frac{p_2^{\alpha_2 - 1}(1-p_2)^{\beta_2 - 1}}{B(\alpha_2, \beta_2)} \\ & = \frac{B(\alpha_1 + k, \beta_1)}{B(\alpha_1, \beta_1)} \underbrace{\int_0^1\!\!\!\!dp_1 \frac{p_1^{\alpha_1 + k - 1}(1-p_1)^{\beta_1 - 1}}{B(\alpha_1 + k, \beta_1)}}_1 \cdot \frac{B(\alpha_2 - k, \beta_2)}{B(\alpha_2, \beta_2)} \underbrace{\int_0^1 \!\!\!\!dp_2 \frac{p_2^{\alpha_2 - k - 1}(1-p_2)^{\beta_2 - 1}}{B(\alpha_2 - k, \beta_2)}}_1 \\ & = \frac{B(\alpha_1 + k, \beta_1)}{B(\alpha_1, \beta_1)} \cdot \frac{B(\alpha_2 - k, \beta_2)}{B(\alpha_2, \beta_2)} \end{align*}\]

where the integrals have each been recognized as the normalization integral of a Beta distribution, and hence are 1. The remaining Beta functions can be simplified by expanding into Gamma functions, and using the Gamma recurrence relation:

\[\begin{align*} B(\alpha, \beta) & = \frac{\Gamma(\alpha)\Gamma(\beta)}{\Gamma(\alpha + \beta)} \\ \Gamma(n + 1) & = n \Gamma(n) \end{align*}\]

So we then get:

\[\begin{align*} E\left[R^k\right] & = \frac{\Gamma(\alpha_1 + k)\Gamma(\beta_1)}{\Gamma(\alpha_1 + \beta_1 + k)} \cdot \frac{\Gamma(\alpha_1 + \beta_1)}{\Gamma(\alpha_1) \Gamma(\beta_1)} \cdot \frac{\Gamma(\alpha_2 - k)\Gamma(\beta_2)}{\Gamma(\alpha_2 + \beta_2 - k)} \cdot \frac{\Gamma(\alpha_2 + \beta_2)}{\Gamma(\alpha_2) \Gamma(\beta_2) } \\ & = \frac{\Gamma(\alpha_1 + k)}{\Gamma(\alpha_1)} \cdot \frac{\Gamma(\alpha_1 + \beta_1)}{\Gamma(\alpha_1 + \beta_1 + k)} \cdot \frac{\Gamma(\alpha_2 - k)}{\Gamma(\alpha_2)} \cdot \frac{\Gamma(\alpha_2 + \beta_2)}{\Gamma(\alpha_2 + \beta_2 - k)} \\ & = \frac{(\alpha_1)_k}{(\alpha_1 + \beta_1)_k} \cdot \frac{\Gamma(\alpha_2 - k)}{\Gamma(\alpha_2)} \cdot \frac{\Gamma(\alpha_2 + \beta_2)}{\Gamma(\alpha_2 + \beta_2 - k)} \end{align*}\]

where we’ve recognized in the first 2 Gamma ratios the rising Pochammer symbols defined above. The remaining 2 Gamma ratios will require a bit of thought, but unsurprisingly they turn out to be expressible in terms of Pochammer symbols as well:

\[\begin{align*} \frac{\Gamma(a-k)}{\Gamma(a)} &= \frac{\Gamma(a-k)}{(a-1)\Gamma(a-1)} \\ &= \frac{\Gamma(a-k)}{(a-1)(a-2)\Gamma(a-2)} \\ &= \frac{\Gamma(a-k)}{(a-1)(a-2)\cdots(a-k)\Gamma(a-k)} \\ &= \frac{1}{(a-k)_k} \end{align*}\]

So our final expression for the $k^\mbox{th}$ moment of $R$ is:

\[E\left[R^k\right] = \frac{(\alpha_1)_k}{(\alpha_1 + \beta_1)_k} \cdot \frac{(\alpha_2 + \beta_2 - k)_k}{(\alpha_2 - k)_k}\]

In particular, the case $k = 0$ gives us the correct answer of 1 for the $0^\mbox{th}$ moment, and the case $k = 1$ gives us the mean of the ratio distribution:

\[E\left[R\right] = \frac{\alpha_1}{\alpha_1 + \beta_1} \cdot \frac{\alpha_2 + \beta_2 - 1}{\alpha_2 - 1}\]

(NB: The median is a bit more interesting than the mean when the distribution is highly skewed, but we couldn’t figure out a closed form result for the median. We’ll just have to be satisfied with using the CDF below and a bit of numerics to find the 50% quantile.)

Continuity at $R = 1$

Pham-Gia did not address in his paper whether the 2 different expressions for $\Pr(R)$ matched up at $R = 1$, i.e., that the probability distribution is continuous. We can show that the above expressions for $\Pr(R | 0 \le R \le 1)$ and $\Pr(R | 1 \lt R)$ are equal in the left and right limits approaching $R = 1$, establishing continuity at that point.

We need 2 identities:

• From Wikipedia’s entry on ${}{2}F_{1}()$ and values at special points comes an identity for evaluating ${}_{2}F_{1}()$ at 1, provided $\Re(c) \gt \Re(a+b)$. For the positive values of $\alpha_i, \beta_i$ we’re considering, this is the case so:

\[{}_{2}F_{1}(a,b;c;1) = \frac{\Gamma(c) \Gamma(c-a-b)}{\Gamma(c-a) \Gamma(c-b) }\]

• Also, we need to decompose complete Beta functions into Gamma functions, via the standard identity we all learned at our mother’s knees:

\[B(a, b) = \frac{\Gamma(a) \Gamma(b)}{\Gamma(a+b)}\]

Case $0 \le R \le 1$:

\[\begin{align*} \Pr(R | 0 \le R \le 1) &\xrightarrow[R \to 1^{-}]{} \frac{B(\alpha_1 + \alpha_2, \beta_2)}{B(\alpha_1, \beta_1) B(\alpha_2, \beta_2)} \frac{\Gamma(\alpha_1 + \alpha_2 + \beta_2) \Gamma(\beta_1 + \beta_2 - 1)}{\Gamma(\beta_2) \Gamma(\alpha_1 + \alpha_2 + \beta_1 + \beta_2 - 1)} \\ &= \frac{1}{B(\alpha_1, \beta_1) B(\alpha_2, \beta_2)} \frac{\Gamma(\alpha_1 + \alpha_2) \Gamma(\beta_2)}{\Gamma(\alpha_1 + \alpha_2 + \beta_2)} \frac{\Gamma(\alpha_1 + \alpha_2 + \beta_2) \Gamma(\beta_1 + \beta_2 - 1)}{\Gamma(\beta_2) \Gamma(\alpha_1 + \alpha_2 + \beta_1 + \beta_2 - 1)} \\ &= \frac{1}{B(\alpha_1, \beta_1) B(\alpha_2, \beta_2)} \frac{\Gamma(\alpha_1 + \alpha_2)\Gamma(\beta_1 + \beta_2 - 1)}{\Gamma(\alpha_1 + \alpha_2 + \beta_1 + \beta_2 - 1)} \\ &= \frac{B(\alpha_1 + \alpha_2, \beta_1 + \beta_2 - 1)}{B(\alpha_1, \beta_1) B(\alpha_2, \beta_2)} \end{align*}\]

Case $1 \le R$:

\[\begin{align*} \Pr(R | 0 \le R \le 1) &\xrightarrow[R \to 1^{+}]{} \frac{B(\alpha_1 + \alpha_2, \beta_1)}{B(\alpha_1, \beta_1) B(\alpha_2, \beta_2)} \frac{\Gamma(\alpha_1 + \alpha_2 + \beta_1)\Gamma(\beta_1 + \beta_2 - 1)}{\Gamma(\beta_1)\Gamma(\alpha_1 + \alpha_2 + \beta_1 + \beta_2 - 1)} \\ &= \frac{1}{B(\alpha_1, \beta_1) B(\alpha_2, \beta_2)} \frac{\Gamma(\alpha_1 + \alpha_2)\Gamma(\beta_1)}{\Gamma(\alpha_1 + \alpha_2 + \beta_1)} \frac{\Gamma(\alpha_1 + \alpha_2 + \beta_1)\Gamma(\beta_1 + \beta_2 - 1)}{\Gamma(\beta_1)\Gamma(\alpha_1 + \alpha_2 + \beta_1 + \beta_2 - 1)} \\ &= \frac{1}{B(\alpha_1, \beta_1) B(\alpha_2, \beta_2)} \frac{\Gamma(\alpha_1 + \alpha_2)\Gamma(\beta_1 + \beta_2 - 1)}{\Gamma(\alpha_1 + \alpha_2 + \beta_1 + \beta_2 - 1)} \\ &= \frac{B(\alpha_1 + \alpha_2, \beta_1 + \beta_2 -1)}{B(\alpha_1, \beta_1) B(\alpha_2, \beta_2)} \end{align*}\]

These 2 expressions being identical, we have established continuity at $R = 1$.

Smoothness at $R = 1$

We’d like to believe that in addition to being continuous at $R = 1$, the PDF is also smooth, i.e., some rather large number of derivatives are also continuous. There is no particular reason to expect a kink in the PDF here, so it would be nice to know that our piecewise representation of the PDF has not introduced a kink.

This requires differentiating ${}_{2}F_{1}(a, b; c; z)$ with respect to $z$. One can stare at Wikipedia’s hypergeometric function differentiation formulas, or just differentiate the power series above to get the same answer: the derivative of a hypergeometric function is a constant times another hypergeometric function, with +1 added to the parameters:

\[\begin{alignat*}{4} \frac{d}{dz} &{}_{2}F_{1}(a,b;c;z) &&= \frac{ab}{c} &\times&{}_{2}F_{1}(a+1, b+1; c+1; z) \\ \frac{d^2}{dz^2} &{}_{2}F_{1}(a,b;c;z) &&= \frac{a(a+1)b(b+1)}{c(c+1)} &\times&{}_{2}F_{1}(a+2, b+2; c+2; z) \\ & && \vdots & \\ \frac{d^n}{dz^n} &{}_{2}F_{1}(a,b;c;z) &&= \frac{(a)_n (b)_n}{(c)_n} &\times&{}_{2}F_{1}(a+n, b+n; c+n; z) \end{alignat*}\]

… where the last expression for the derivative in the general case again uses the rising Pochammer symbols, just as above in the series definition of ${}_{2}F_{1}(a, b; c; z)$.

While it’s tempting to do the general case of the $n^\mathrm{th}$ derivative to show it’s $C^\infty$ smooth, we’ll content ourselves here with just the first derivative and the knowledge there’s no kink at $R = 1$.

We’ll assemble the goods from 6 identities for the piecewise definition of our distribution, how to differentiate it, a formula for the value at unity of ${}_2F_{1}(\cdots; 1)$, and some lore of $B()$ and $\Gamma$ functions, all assemblere here in one spot for quick reference:

\[\begin{align*} \Pr(R | 0 \le R \le 1) &= \frac{B(\alpha_1 + \alpha_2, \beta_2)}{B(\alpha_1, \beta_1) B(\alpha_2, \beta_2)} \cdot R^{\alpha_1 - 1} \cdot {}_2F_1(\alpha_1 + \alpha_2, 1 - \beta_1; \alpha_1 + \alpha_2 + \beta_2; R) \\ \Pr(R | 1 \lt R) &= \frac{B(\alpha_1 + \alpha_2, \beta_1)}{B(\alpha_1, \beta_1) B(\alpha_2, \beta_2)} \cdot \frac{1}{R^{\alpha_2 + 1}} \cdot {}_2F_1(\alpha_1 + \alpha_2, 1 - \beta_2; \alpha_1 + \alpha_2 + \beta_1; 1/R) \\ \frac{d}{dz} {}_{2}F_{1}(a,b;c;z) &= \frac{ab}{c} \times{}_{2}F_{1}(a+1, b+1; c+1; z) \\ {}_2F_1(a, b; c; 1) &= \frac{\Gamma(c) \Gamma(c-a-b)}{\Gamma(c-a) \Gamma(c-b)} \\ B(\alpha, \beta) &= \frac{\Gamma(\alpha) \Gamma(\beta)}{\Gamma(\alpha + \beta)} \\ \Gamma(n + 1) &= n \Gamma(n) \end{align*}\]

Case $0 \le R \le 1$:

\[\begin{align*} &\frac{d}{dR} \Pr(R | 0 \le R \le 1)&& \\ &= \frac{B(\alpha_1 + \alpha_2, \beta_2)}{B(\alpha_1, \beta_1) B(\alpha_2, \beta_2)} \times&&\frac{d}{dR} \left[R^{\alpha_1 - 1} \cdot {}_2F_1(\alpha_1 + \alpha_2, 1 - \beta_1; \alpha_1 + \alpha_2 + \beta_2; R)\right] \\ &= \frac{B(\alpha_1 + \alpha_2, \beta_2)}{B(\alpha_1, \beta_1) B(\alpha_2, \beta_2)} \times&&\left[ (\alpha_1 - 1) R^{\alpha_1 - 2} {}_2F_1(\alpha_1 + \alpha_2, 1 - \beta_1; \alpha_1 + \alpha_2 + \beta_2; R) \right. \\ &&& \left. + R^{\alpha_1 - 1} \frac{(\alpha_1 + \alpha_2)(1 - \beta_1)}{\alpha_1 + \alpha_2 + \beta_2} {}_2F_1(\alpha_1 + \alpha_2 + 1, 2-\beta_1; \alpha_1 + \alpha_2 + \beta_2 + 1; R)\right] \\ &\xrightarrow[R \to 1^{-}]{} \frac{B(\alpha_1 + \alpha_2, \beta_2)}{B(\alpha_1, \beta_1)B(\alpha_2, \beta_2)} \times &&\left[(\alpha_1 - 1) \frac{\Gamma(\alpha_1 + \alpha_2 + \beta_2) \Gamma(\beta_1 + \beta_2 -1)}{\Gamma(\beta_2)\Gamma(\alpha_1 + \alpha_2 + \beta_1 + \beta_2 - 1)} \right. \\ &&& \left. + \frac{(\alpha_1 + \alpha_2)(1 - \beta_1)}{\alpha_1 + \alpha_2 + \beta_2} \frac{\Gamma(\alpha_1 + \alpha_2 + \beta_2 + 1)\Gamma(\beta_1 + \beta_2 - 2)}{\Gamma(\beta_2)\Gamma(\alpha_1 + \alpha_2 + \beta_1 + \beta_2 - 1)} \right] \\ &= \frac{B(\alpha_1 + \alpha_2, \beta_2)}{B(\alpha_1, \beta_1) B(\alpha_2, \beta_2)} \times &&\frac{\Gamma(\alpha_1 + \alpha_2 + \beta_2)\Gamma(\beta_1 + \beta_2 - 2)}{\Gamma(\beta_2)\Gamma(\alpha_1 + \alpha_2 + \beta_1 + \beta_2 - 1)} \\ &&&\times \left[(\alpha_1 - 1)(\beta_1 + \beta_2 - 2) + (\alpha_1 + \alpha_2)(1 - \beta_1)\right] \\ &= \frac{1}{B(\alpha_1, \beta_1) B(\alpha_2, \beta_2)} \times &&\frac{\Gamma(\alpha_1 + \alpha_2)\Gamma(\beta_2)}{\Gamma(\alpha_1 + \alpha_2 + \beta_2)} \times \frac{\Gamma(\alpha_1 + \alpha_2 + \beta_2)\Gamma(\beta_1 + \beta_2 - 2)}{\Gamma(\beta_2)\Gamma(\alpha_1 + \alpha_2 + \beta_1 + \beta_2 - 1)} \\ &&&\times \left[(\alpha_1 - 1)(\beta_1 + \beta_2 - 2) + (\alpha_1 + \alpha_2)(1 - \beta_1)\right] \\ &= \frac{B(\alpha_1 + \alpha_2, \beta_1 + \beta_2 - 1)}{B(\alpha_1, \beta_1) B(\alpha_2, \beta_2)} \times &&\frac{(\alpha_1 - 1) (\beta_1 + \beta_2 - 2) + (\alpha_1 + \alpha_2) (1 - \beta_1)}{\beta_1 + \beta_2 - 2} \\ &= \frac{B(\alpha_1 + \alpha_2, \beta_1 + \beta_2 - 1)}{B(\alpha_1, \beta_1) B(\alpha_2, \beta_2)} \times &&\frac{\alpha_1\beta_2 - \alpha_2\beta_1 + \alpha_2 - \alpha_1 - \beta_1 -\beta_2 + 2}{\beta_1 + \beta_2 - 2} \\ &= \frac{B(\alpha_1 + \alpha_2, \beta_1 + \beta_2 - 1)}{B(\alpha_1, \beta_1) B(\alpha_2, \beta_2)} \times &&\left[\frac{\alpha_1\beta_2 - \alpha_2\beta_1 + \alpha_2 - \alpha_1}{\beta_1 + \beta_2 - 2} - 1\right] \end{align*}\]

Case $1 \le R$:

\[\begin{align*} &\frac{d}{dR} \Pr(R | 1 \lt R)&& \\ &= \frac{B(\alpha_1 + \alpha_2, \beta_1)}{B(\alpha_1, \beta_1) B(\alpha_2, \beta_2)} \times &&\frac{d}{dR} \left[\frac{1}{R^{\alpha_2 + 1}} {}_{2}F_{1}(\alpha_1 + \alpha_2, 1-\beta_2; \alpha_1 + \alpha_2 + \beta_1; 1/R) \right] \\ &= \frac{B(\alpha_1 + \alpha_2, \beta_1)}{B(\alpha_1, \beta_1) B(\alpha_2, \beta_2)} \times &&\left[-\frac{\alpha_2 + 1}{R^{\alpha_2 + 2}} {}_2F_1(\alpha_1 + \alpha_2, 1-\beta_2; \alpha_1 + \alpha_2 + \beta_1; 1/R) \right. \\ &&& \left. + \frac{1}{R^{\alpha_2 + 1}} \frac{(\alpha_1 + \alpha_2)(1-\beta_2)}{\alpha_1 + \alpha_2 + \beta_1} {}_{2}F_{1}(\alpha_1 + \alpha_2 + 1, 2 - \beta_2; \alpha_1 + \alpha_2 + \beta_1 + 1; 1/R) \left(-\frac{1}{R^2}\right)\right] \\ &\xrightarrow[R \to 1^{+}]{} \frac{B(\alpha_1 + \alpha_2, \beta_1)}{B(\alpha_1, \beta_1) B(\alpha_2, \beta_2)} \times &&\left[ -(\alpha_2 + 1) \frac{\Gamma(\alpha_1 + \alpha_2 + \beta_1) \Gamma(\beta_1 + \beta_2 - 1)}{\Gamma(\beta_1) \Gamma(\alpha_1 + \alpha_2 + \beta_1 + \beta_2 - 1)} \right. \\ &&& \left. - \frac{(\alpha_1 + \alpha_2)(1-\beta_2)}{\alpha_1 + \alpha_2 + \beta_1} \frac{\Gamma(\alpha_1 + \alpha_2 + \beta_1 + 1)\Gamma(\beta_1 + \beta_2 - 2)}{\Gamma(\beta_1)\Gamma(\alpha_1 + \alpha_2 + \beta_1 + \beta_2 - 1)}\right] \\ &= \frac{B(\alpha_1 + \alpha_2, \beta_1)}{B(\alpha_1, \beta_1) B(\alpha_2, \beta_2)}\times&& \frac{\Gamma(\alpha_1 + \alpha_2 + \beta_1)\Gamma(\beta_1 + \beta_2 - 2)}{\Gamma(\beta_1)\Gamma(\alpha_1 + \alpha_2 + \beta_1 + \beta_2 - 1)} \\ &&& \times \left[-(\alpha_2 + 1)(\beta_1 + \beta_2 - 2) - (\alpha_1 + \alpha_2)(1 - \beta_2)\right] \\ &= \frac{1}{B(\alpha_1, \beta_1) B(\alpha_2, \beta_2)} \times && \frac{\Gamma(\alpha_1 + \alpha_2)\Gamma(\beta_1)}{\Gamma(\alpha_1 + \alpha_2 + \beta_1)} \times \frac{\Gamma(\alpha_1 + \alpha_2 + \beta_1)\Gamma(\beta_1 + \beta_2 - 2)}{\Gamma(\beta_1)\Gamma(\alpha_1 + \alpha_2 + \beta_1 + \beta_2 - 1)} \\ &&& \left[-(\alpha_2 + 1)(\beta_1 + \beta_2 - 2) - (\alpha_1 + \alpha_2)(1 - \beta_2)\right] \\ &= \frac{B(\alpha_1 + \alpha_2, \beta_1 + \beta_2 -1)}{B(\alpha_1, \beta_1) B(\alpha_2, \beta_2)} \times && \frac{-(\alpha_2 + 1)(\beta_1 + \beta_2 - 2) - (\alpha_1 + \alpha_2)(1 - \beta_2)}{\beta_1 + \beta_2 - 2} \\ &= \frac{B(\alpha_1 + \alpha_2, \beta_1 + \beta_2 -1)}{B(\alpha_1, \beta_1) B(\alpha_2, \beta_2)} \times && \frac{\alpha_1 \beta_2 - \alpha_2 \beta_1 + \alpha_2 - \alpha_1 - \beta_1 - \beta_2 + 2}{\beta_1 + \beta_2 - 2} \\ &= \frac{B(\alpha_1 + \alpha_2, \beta_1 + \beta_2 -1)}{B(\alpha_1, \beta_1) B(\alpha_2, \beta_2)} \times && \left[\frac{\alpha_1 \beta_2 - \alpha_2 \beta_1 + \alpha_2 - \alpha_1}{\beta_1 + \beta_2 - 2} - 1\right] \end{align*}\]

Those two derivative expressions being identical, we have established equality of the first derivatives at $R = 1$, so our distribution is first-order smooth.

Ok, but what about the cumulative distribution function?

That gives us the PDF (probability distribution function); if we want the CDF (cumulative distribution function) to calculate quantiles, we’ll have to go beyond Pham-Gia’s paper. That’s the accumulated probability from $0$ to $R_0$, $\Pr(\lt R_0)$, which we get by integrating. Since the PDF is piecewise, so is the CDF. We get the piece for $R \lt R_0$ by integrating from $0$ to $R_0$, and the piece for $R_0 \gt 1$ by integrating back from $+\infty$ to $R_0$, and subtracting from 1:

\[\begin{align*} \Pr( \lt R_0 | 0 \le R_0 \le 1) &= \int_0^{R_0}\!\!\!\!\!\!dR \Pr(R | 0 \le R \le 1) \\ &= \frac{B(\alpha_1 + \alpha_2, \beta_2)}{B(\alpha_1, \beta_1) B(\alpha_2, \beta_2)} \int_0^{R_0}\!\!\!\!\!\!dR \: R^{\alpha_1 - 1} {}_2F_1(\alpha_1 + \alpha_2, 1 - \beta_1; \alpha_1 + \alpha_2 + \beta_2; R) \\ \Pr( \lt R_0 | 1 \lt R_0) &= 1 - \int_{R_0}^{+\infty}\!\!\!\!\!\!\!\!\!dR \Pr(R | 1\lt R) \\ &= 1 - \frac{B(\alpha_1 + \alpha_2, \beta_1)}{B(\alpha_1, \beta_1) B(\alpha_2, \beta_2)} \int_{R_0}^{+\infty}\!\!\!\!\!\!\!\!\!dR \frac{1}{R^{\alpha_2 + 1}} {}_2F_1(\alpha_1 + \alpha_2, 1 - \beta_2; \alpha_1 + \alpha_2 + \beta_1; 1/R) \end{align*}\]

That leaves us with the riddle of how to integrate powers times ${}_2F_{1}()$’s, and the inverse version of that (which is probably equivalent to the first integral, after a change of variables).

We address the first integral by hitting up the power series:

\[\begin{align*} \int_0^{y \lt 1}\!\!\!\!dx \: x^d {}_2F_1(a, b; c; x) &= \int_0^{y \lt 1}\!\!\!\!dx \: x^d \sum_{n=0}^{+\infty} \frac{(a)_n (b)_n}{(c)_n} \frac{x^n}{n!} \\ &= \sum_{n=0}^{+\infty} \frac{(a)_n (b)_n}{(c)_n} \frac{1}{n!} \int_0^{y \lt 1}\!\!\!\!dx \: x^{n+d} \\ &= \sum_{n=0}^{+\infty} \frac{(a)_n (b)_n}{(c)_n} \frac{1}{n!} \left.\frac{x^{n+d+1}}{n+d+1}\right|_0^{y \lt 1} \\ &= \frac{y^{d+1}}{d+1} \sum_{n=0}^{+\infty} \frac{(a)_n (b)_n}{(c)_n} \frac{d+1}{n+d+1} \frac{y^n}{n!} \\ &= \frac{y^{d+1}}{d+1} \sum_{n=0}^{+\infty} \frac{(d+1)_n (a)_n (b)_n}{(d+2)_n (c)_n} \frac{y^n}{n!} \\ &= \frac{y^{d+1}}{d+1} {}_3F_2(d+1, a, b; d+2, c; y) \end{align*}\]

where the lower limit of the integral vanishes if $d > -1$ (as assumed here), has a constant from ${}_{3}F_{2}(0)$ if $d = -1$, and has a pole if $d < -1$.

We’ve recognized in the series the generalized hypergeometric function ${}_{3}F_{2}()$. The subscripts remind us that there are 3 Pochammer symbols in the numerator and 2 in the denominator, vs 2 in the numerator and 1 in the denominator for ${}_{2}F_{1}()$.

Ok, we have a little fear and trembling at the sight of ${}_{3}F_{2}()$ (having summoned up that which which we might not be able to put down). Nonetheless, we swallow our fears and proceed recklessly to the second integral via a change of variables:

\[\begin{align*} x &= 1/u \\ x &= - du/u^2 \end{align*}\]

which turns out to just transform this back into the first case:

\[\begin{align*} \int_{y \gt 1}^{+\infty}\!\!\!\!\!\!\!\!\!dx \frac{1}{x^d} {}_2F_1(a,b;c; 1/x) &= \int_{0}^{(1/y) \lt 1}\!\!\!\!\!\!\!\!\!du \:\frac{1}{u^2} u^d {}_2F_1(a, b; c; u) \\ &= \int_{0}^{(1/y) \lt 1}\!\!\!\!\!\!\!\!\!du \:u^{d-2} u^d {}_2F_1(a, b; c; u) \\ &= \left.\frac{u^{d-1}}{d-1} {}_3F_2(d-1, a, b; d, c; u) \right|_0^{(1/y) \lt 1} \\ &= \frac{1}{(d-1)y^{d-1}} {}_3F_2(d-1, a, b; d, c; 1/y) \end{align*}\]

where the lower limit vanishes at 0 if $d \gt 1$ (as assumed here), is a constant from if ${}_{3}F_{2}(0)$ if $d = 1$, and has a pole if $d \lt 1$.

Armed with those 2 hypergeometric integrals, we can now read off the piecewise CDF from the definitions above:

\[\begin{align*} \Pr( \lt R_0 | 0 \le R_0 \le 1) &= \int_0^{R_0}\!\!\!\!\!\!dR \Pr(R | 0 \le R \le 1) \\ &= \frac{B(\alpha_1 + \alpha_2, \beta_2)}{B(\alpha_1, \beta_1) B(\alpha_2, \beta_2)} \int_0^{R_0}\!\!\!\!\!\!dR \: R^{\alpha_1 - 1} {}_2F_1(\alpha_1 + \alpha_2, 1 - \beta_1; \alpha_1 + \alpha_2 + \beta_2; R) \\ &= \frac{B(\alpha_1 + \alpha_2, \beta_2)}{B(\alpha_1, \beta_1) B(\alpha_2, \beta_2)} \frac{R_0^{\alpha_1}}{\alpha_1} {}_3F_2(\alpha_1, \alpha_1 + \alpha_2, 1 - \beta_1;\alpha_1 + 1, \alpha_1 + \alpha_2 + \beta_2; R_0) \\ &\xrightarrow[R_0 \to 0]{} 0 \checkmark \\ & \\ \Pr( \lt R_0 | 1 \lt R_0) &= 1 - \int_{R_0}^{+\infty}\!\!\!\!\!\!\!\!\!dR \Pr(R | 1\lt R) \\ &= 1 - \frac{B(\alpha_1 + \alpha_2, \beta_1)}{B(\alpha_1, \beta_1) B(\alpha_2, \beta_2)} \int_{R_0}^{+\infty}\!\!\!\!\!\!\!\!\!dR \frac{1}{R^{\alpha_2 + 1}} {}_2F_1(\alpha_1 + \alpha_2, 1 - \beta_2; \alpha_1 + \alpha_2 + \beta_1; 1/R) \\ &= 1 - \frac{B(\alpha_1 + \alpha_2, \beta_1)}{B(\alpha_1, \beta_1) B(\alpha_2, \beta_2)} \frac{1}{\alpha_2 R_0^{\alpha_2}} {}_3F_2(\alpha_2, \alpha_1 + \alpha_2, 1 - \beta_2; \alpha_2 + 1, \alpha_1 + \alpha_2 + \beta_1; 1/R_0) \\ &\xrightarrow[R_0 \to +\infty]{} 1 \checkmark \\ \end{align*}\]

The appropriate limits as $R_0 \rightarrow 0$ and as $R_0 \rightarrow +\infty$ are manifest, due to the way we structured the integrals.

However, since we have a piecewise CDF, we have to show it’s continuous at the piece boundary at $R = 1$. (It must be, since it’s the integral of the PDF which we showed above is continuous and first-order smooth. We just want to be sure!)

That amounts to proving the following equality, joining the values of the CDF from below and above 1:

\[\begin{align*} & \frac{B(\alpha_1 + \alpha_2, \beta_2)}{B(\alpha_1, \beta_1) B(\alpha_2, \beta_2)} \frac{1}{\alpha_1} {}_3F_2(\alpha_1, \alpha_1 + \alpha_2, 1 - \beta_1; \alpha_1 + 1, \alpha_1 + \alpha_2 + \beta_2; 1) \\ + & \frac{B(\alpha_1 + \alpha_2, \beta_1)}{B(\alpha_1, \beta_1) B(\alpha_2, \beta_2)} \frac{1}{\alpha_2} {}_3F_2(\alpha_2, \alpha_1 + \alpha_2, 1 - \beta_2; \alpha_2 + 1, \alpha_1 + \alpha_2 + \beta_1; 1) \\ = & 1 \end{align*}\]

So we need to hunt down some identities for ${}_{3}F_{2}(1)$ at various parameter values. We have not as yet figured out how to do that. …TBD…

To summarize the CDF result:

\[\left\{ \begin{alignat*}{8} \Pr( \lt R_0 | 0 \le R_0 \le 1) &= & \frac{B(\alpha_1 + \alpha_2, \beta_2)}{B(\alpha_1, \beta_1) B(\alpha_2, \beta_2)} &\cdot&& \frac{R_0^{\alpha_1}}{\alpha_1} &\cdot& {}_3F_2(\alpha_1, \alpha_1 + \alpha_2, 1 - \beta_1;\alpha_1 + 1, \alpha_1 + \alpha_2 + \beta_2; R_0) \\ \Pr( \lt R_0 | 1 \lt R_0) &= 1 - & \frac{B(\alpha_1 + \alpha_2, \beta_1)}{B(\alpha_1, \beta_1) B(\alpha_2, \beta_2)} &\cdot&& \frac{1}{\alpha_2 R_0^{\alpha_2}} &\cdot& {}_3F_2(\alpha_2, \alpha_1 + \alpha_2, 1 - \beta_2; \alpha_2 + 1, \alpha_1 + \alpha_2 + \beta_1; 1/R_0) \end{alignat*} \right.\]

A Second Opinion

Now, it turns out that Julian Saffer has already worked this out, and what’s more put a library in Python on Github. ^[3] Now, I’m not so much with the Python; I’m more of an R guy. But let’s have a look.

In Saffer’s notation, what we call the ratio $R$ he calls $w$. His integrals agree with ours:

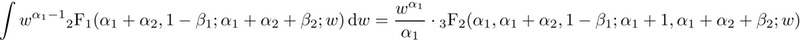
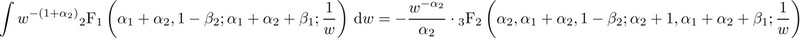
Also, his use of those integrals gets a piecewise CDF which is also identical to ours. For $0 \le w \le 1$:

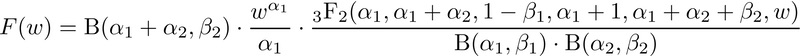
And for $w > 1$:

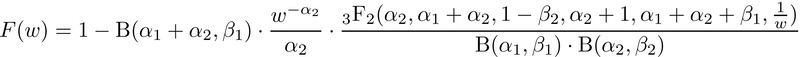
I’m a bit suspicious of his Python code, since:

• Hey, I’m an R guy. Of course I’m a bit uneasy with Python stuff.
• He calculates things in log space and then exponentiates. This makes some sense, to avoid large factorials, but it also exponentiates roundoff errors in a numerically unstable way. Better to use a recursion relation on the series coefficients, and transformations to get the argument to be as small as possible on the real line. (We’re not so concerned about the complex plane here.)
• He does not address what happens when the parameters $a, b, c$ of the hypergeometric functions become large. To analyze the Pfizer or Moderna vaccine trials, these can be order of 10s of thousands! Clearly some sort of recurrence relation is needed to lower the order there.

But we can test against his Python code on a low order example and see if we agree. Fortunately, Saffer provides exactly such an example. (This is how good science proceeds, by seeing if independent assessment agree.)

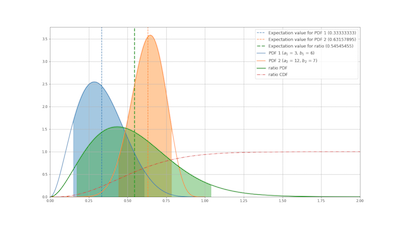
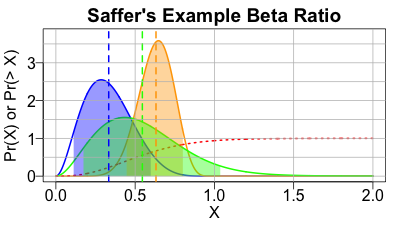
Saffer’s repository shows a graph with an example of a numerator Beta distribution with $\alpha_ 1 = 3, \beta_1 = 6$ and a denominator Beta distribution with $\alpha_ 1 = 12, \beta_1 = 7$. These values won’t trigger any of our concerns about large-parameter evaluation of hypergeometric or generalized hypergeometric functions. So let’s compare.

The top graph here is from Saffer’s repository. He shows:

• the PDF of the numerator, its 90% confidence interval, and its mean (blue),
• the PDF of the denominator, its 90% confidence interval, and its mean (orange),
• the PDF of the ratio, its 90% confidence interval, and its mean (green),
• the CDF of the ratio (red)

The second graph here uses our formulae above and a naive implementation using the R package hypergeo, to reproduce the graph as best we can. ^[4]

We note with some satisfaction that the graphs are more or less identical. Apparently we’re calculating the same thing: we may be wrong, but if so, we’re wrong together. So, at least for relatively smallish values of the hypergeometric parameters $a, b, c$ we agree. It will be another matter to make this practical for numeric stability for large values of $a, b, c$.

Computational realization for practical use

At some point soon, I’d like to implement this in R. There are some gnarly issues with numerical roundoff. Even though the hypergeometric series terminates as a polynomial for integer $\beta$’s, one simply cannot naïvely compute a polynomial of order 15,000 for a large clinical trial and expect to get anything other than nonsense!

That’s work for another day.

The Weekend Conclusion

In a spirit of proper collegiality, I wish to acknowledge warmly the assistance of the Weekend Publisher at several points in this analysis. He provided encouragement when I wanted to give up. He is shown here in mid-critique, providing valuable purr review.

That acknowledgement having been made, we’ve worked our way through the relevant parts of Pham-Gia’s paper (though there’s a lot more there!), and confirmed the primary result that the PDF of the ratio of 2 independent Beta-distributed random variables is a variety of hypergeometric function ${}_{2}F_{1}()$.

Somewhat beyond Pham-Gia’s paper, we’ve also proven the continuity of the PDF at $R = 1$, i.e., that the expression for $0 \le R \le 1$ and the one for $R \gt 1$ match up at $R = 1$.

We’ve also derived the CDF in a similarly piecewise way, to be used for calculating quantiles. Our results match those of Saffer, so we’re probably on the right track here.

However, there are several things we haven’t done:

• While we’ve shown continuity and first-order smoothness (non-kink) at $R = 1$, we suspect a much stronger condition of $C^{\infty}$ smoothness holds. To prove that, we’d have to match all derivatives, but we’ve only done orders 0 and 1 here.
• While we have the CDF function, we haven’t demonstrated continuity at $R = 1$. That requires some identities about ${}_{3}F_{2}(1)$ for various parameter values.
• We also haven’t wrestled with all the numeric issues of implementing this, say in R. However, for relatively small values of the parametes, we’ve managed to reproduce convincingly the example Saffer reports in his repository.
• Furthermore, we haven’t investigated the quantile function (functional inverse of the CDF) which would let us read off quantiles directly. Looking at Saffer’s code, he hasn’t either: he’s using Newton’s method to solve the relevant equation directly from the CDF, which is totally fair.

So we’ve got a bit more work to do to make this useable in a practical sense.

---

Notes & References

1: T Pham-Gia, “Distributions of the ratios of independent beta variables and applications”, Comm Stat: Theory & Methods, 29:12, 2693-2715. DOI: 10.1080/03610920008832632. Since it was so hard to get, I’ve archived a copy here.

NB: We believe there are several errata in this paper which make it much harder to read than need be. We’ve worked through the details, and with these corrections, obtain the same eventual result in terms of ${}_{2}F_{1}()$. Specifically:

• p. 2696, in the definition of the Pochammer coefficients: $K$ should be $\ldots$
• p. 2698, in the equation for the marginal density $f(w)$:
  • The upper limit of integration should be $+1$, not $+\infty$
  • The exponent of $(1-x_2)$ should be $\beta_{2}-1$, not $\beta_{2}$
• p. 2698, in the integral for $f(w)$ for $0 \le w \le 1$:
  • the integration measure is missing, and should be $dx_2$
  • in the rightmost expression, the exponent of $(1-x_2)$ should again be $\beta_{2}-1$, not $\beta_{2}$
• p. 2703, in the variables for a Dirichlet distribution, $K$ should again be $\ldots$

While there may or may not be similar typos (almost certainly due to journal typesetting, not Pham-Gia, who seems to be a pretty good guy!) in the rest of the paper, we haven’t checked carefully since it does not bear directly on our interests. But with the corrigenda above, we were able to reproduce Pham-Gia’s main result, the piecewise PDF on pp. 2698-2699. ↩

2: OK, the truth is: I was actually a mere 23 years old and in my first year of physics grad school at MIT. I got wrapped around the axle pretty tight, because the notation between various texts was subtly and confusingly different. I thought I’d suddenly become stupid! It took years to get past that. Now, even 45 years later, it’s still a sensitive spot. But… time to face my fears. ↩

3: J Saffer, “Beta Quotient Distribution”, GitHub Repository, last committed 2020-Jun-06, retrieved 2021-Sep-13. ↩

4: Weekend Editor, R script for naive comparison with J Saffer’s example, Some Weekend Reading blog, 2021-Sep-13. ↩