Why did Republicans block a Trump impeachment guilty verdict?
Tagged:MathInTheNews
/
Politics
/
R
/
Statistics
It’s been a couple weeks, so we’ve all calmed down a little. But still… why did 43 Republican senators vote to block the obvious guilty verdict in Trump’s impeachment?
What we’re after
 The Senate has voted: 57 guilty, 43 not guilty. [1] While that’s
a bipartisan supermajority for the guilty vote, it’s not sufficient: 67 guilty votes were
needed (or 15 guilty-voting Republican senators would have had to go stand in the lobby for a few minutes). The facts in evidence were brutally clear. All 50 Democrats and 7 Republicans
acknowledged this. So that raises the question: what were the other 43 Republican senators thinking?!
The Senate has voted: 57 guilty, 43 not guilty. [1] While that’s
a bipartisan supermajority for the guilty vote, it’s not sufficient: 67 guilty votes were
needed (or 15 guilty-voting Republican senators would have had to go stand in the lobby for a few minutes). The facts in evidence were brutally clear. All 50 Democrats and 7 Republicans
acknowledged this. So that raises the question: what were the other 43 Republican senators thinking?!
At some level, I’d like to get inside their heads to understand their thinking. They had to have some way of rationalizing their vote against the facts, perhaps prioritizing political expediency. Was it fear of public retaliation from Trump in the media? Fear of their Trump-addled constituents? Fear of being primaried by some QAnon far to their right in an upcoming reelection campaign? Fear of insufficient tribal loyalty to the Republican tribe?
It could be any of those things, or all in combination. And upon reflection, I really don’t want to “get inside their heads”, because I wouldn’t like what I would find. I’ll leave narrated trips through hell to professionals like Dante, and to his modern admirers, like Niven & Pournelle.
Some possible explanations
Basically, we just elaborate the fears enumerated above, in technical ways that we can actually test statistically:
- To what degree does simple membership in the Republican party force their vote? Given the ideological extremism of the Republicans, this bare fact may foreclose on any other option, all by itself.
- Did a senator vote earlier that the impeachment trial was unconstitutional? While the position is ridiculous – law professors, for example are near-unanimous that it was constitutional – a senator might have wanted to vote “not guilty” out of consistency.
- If Trump won the popular vote in a senator’s state by a large margin, might the senator feel compelled to defend Trump? This could be a misplaced desire to represent constituents even to defending criminality and incompetence. Or it could be they have no stomach to face hordes of Trumpy voters.
- Is the senator running for reelection in 2022? A reelection campaign hot on the heels of impeachment means voters will still remember this vote, and perhaps punish the senator if he voted guilty. If the next campaign is in 2024 or 2026, this may be less the case, as American voters have notoriously and regrettably short memories.
- Is the senator retiring? If so, a senator who doesn’t have to face voters ever again might be able to muster up the courage for a guilty vote.
The available data
Most importantly, we want more than just talk, much more than just story. We want actual statistial evidence for or against these hypotheses. For that, we need data.
Here’s the data we used:
- Votes on the final verdict: We got these from the web pages of the Senate itself [2], slightly rearranged in Emacs for loading into R.
- Votes on the constitutionality of the impeachment trial: Also from the web pages of the Senate itself [3], similarly rearranged for processing by our scripts.
- Popular vote margins in each state: From the table compiled in Wikipedia [4], suitably rearranged for processing by our scripts. Also, we combined the multiple districts into which Maine and Nebraska were broken down into state-wide data. (Those states split electoral votes by congressional district.)
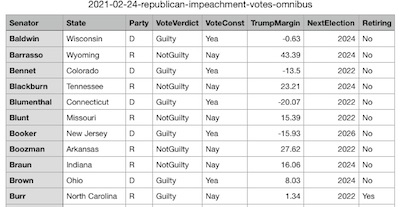
- Reelection ‘classes’ for each senator: Again from the web pages of the Senate itself, describing the ‘class’ for each Senator. Class I is up for reelection in 2024. [5] Class II is up for reelection in 2026. [6] Class III is up for reelection in 2022. [7] It’s this last class which is most likely to feel the heat of angry Trumpy voters in their upcoming reelection campaigns. (There were some amusing issues here. These datasets included spelling some senator’s names with accent marks that dwere not used in the roll call vote reports. Also, there are 2 senators surnamed “Scott”, from Florida and South Carolina. It’s the presence of headaches like this that you know you’re dealing with real data!)
- Senator retirement intentions, as of the impeachment trial date: We assembled these data from 2 sources. The first, from FiveThirtyEight [8], detailed the definitely known retirements of Burr, Toomey, and Portman. The second, from CNN [9], confirmed those and added several “maybe” twists to the data. Significantly, all those flirting with retirement are up for election in 2022, i.e., nobody said “one more time and then I’ll retire”:
| Senator | State | NextElection | Retiring |
|---|---|---|---|
| Burr | North Carolina | 2022 | Yes |
| Grassley | Iowa | 2022 | Maybe |
| Johnson | Wisconsin | 2022 | Maybe |
| Portman | Ohio | 2022 | Yes |
| Shelby | Alabama | 2022 | Maybe |
| Thune | South Dakota | 2022 | Maybe |
| Toomey | Pennsylvania | 2022 | Yes |
 Now, that’s a lot of data sources, and a lot of careful hand manipulation to assemble them
in useful form. So, to facilitate peer review, we’ve written
our analysis script [10] to assemble all of them into a
single, omnibus, tab-separated-value formatted text file [11].
That’s suitable for import into a spreadsheet, or any other analysis tool for peer review
of this analysis.
Now, that’s a lot of data sources, and a lot of careful hand manipulation to assemble them
in useful form. So, to facilitate peer review, we’ve written
our analysis script [10] to assemble all of them into a
single, omnibus, tab-separated-value formatted text file [11].
That’s suitable for import into a spreadsheet, or any other analysis tool for peer review
of this analysis.
Exploratory data analysis
First, let’s look at some crosstabulations to see if there are any interesting hypotheses
to explain the VoteVerdict column from the others.
Looking at VoteConst, the vote for whether the trial was constitutional,
shows the stark breakdown by Party. All Democrats (and 2 Independents who
caucus with them) voted that it was constitutional. All but 6 Republicans voted the other
way. So… yes, there’s a strong partisan divide, but 6 Republicans at least
admitted there was something to do:
Party
VoteConst D I R
Yea 48 2 6
Nay 0 0 44
The same is pretty much true of the final decision in VoteVerdict:
Party
VoteVerdict D I R
Guilty 48 2 7
NotGuilty 0 0 43
And the correlation between VoteConst and VoteVerdict is of
course darn near perfect, since you wouldn’t vote Guilty in a procedure you thought was
constitutional:
VoteConst
VoteVerdict Yea Nay
Guilty 56 1
NotGuilty 0 43
If we dig into the changes, we see that just 1 vote changed between the 2, and it was Senator Burr of North Carolina who is interestingly going to retire in 2022. In news interviews, he said the Democrats changed his mind when the impeachment managers presented such a damning case:
Senator State Party VoteVerdict VoteConst TrumpMargin NextElection Retiring
Burr North Carolina R Guilty Nay 1.34 2022 Yes
Next, let’s look at the breakdown of VoteVerdict versus the next year the
senator has to run for reelection. This looks a little disappointing, like there’s
absolutely no difference in the 2022 class, a significant difference in the 2024 class,
and not much difference in the 2026 class:
NextElection
VoteVerdict 2022 2024 2026
Guilty 17 24 16
NotGuilty 17 9 17
That does not bode well for our hypothesis that senators immediately up for reelection might need to vote “not guilty”! What might be the reason? If we look at the number of seats up for reelection in each year broken down by party, we see the reason. 2024 has a lot more Democratic seats up for reelection by more than 2/3 vs 1/3, while 2022 and 2026 are biased toward Republican seats, though somewhat less so. That would explain why there were so many Guilty votes in the 2024 class:
Party
NextElection D I R
2022 14 0 20
2024 21 2 10
2026 13 0 20
Finally, what about retirements? There are so few, it’s kind of hard to say there’s anything meaningful going on here:
Retiring
VoteVerdict Yes Maybe No
Guilty 2 0 55
NotGuilty 1 4 38
 Finally, we might ask how many independent predictors do we really have here, anyway? It
certainly looks like some of them are heavily correlated! After turning all of them into
numeric variables (turn votes into booleans, and thence into 0/1), we can calculate the
Pearson correlations, as shown.
Finally, we might ask how many independent predictors do we really have here, anyway? It
certainly looks like some of them are heavily correlated! After turning all of them into
numeric variables (turn votes into booleans, and thence into 0/1), we can calculate the
Pearson correlations, as shown.
It looks like there’s 1 block of TrumpMargin, PartyRepublican,
and VotedUnconst that are heavily correlated. This makes sense, and is
really just an expression of party identity.
NotRetiring and Running2022 are less correlated with that block,
and anti-correlated with each other. If I converted to NotRetiring to
Retiring, then they’d be correlated: everybody retiring was going to have to
run in 2022. So that makes sense, too.
Basically, it looks like there are maybe 2 independent predictors here? Or maybe just 1,
if we flip the sign of NotRetiring and note that Running2022 is
mildly positively correlated with the “Trumpy block” of variables.
Machine learning: feature selection
The crosstabulations were not especially encouraging in the quest for explanations beyond
brute-force party identity. Still, let’s press forward. We’ll qualify each of the
columns that might predict VoteVerdict in a univariate regression model. For
example, for the predictor TrumpMargin, we do:
We’ll report the $p$-value for statistial significance of the $\beta_1$ coefficient, for all senators and for just the Republican senators. Then we’ll do a Benjamini-Höchberg multiple hypothesis correction to get the False Discovery Rate. A small(ish) FDR presages that column as a good predictor. The results are intriguing:
Predictor p pRepublican FDR FDRRepublican
1 PartyRepublican 9.92e-01 NA 9.94e-01 NA
2 VotedUnconst 9.94e-01 0.995 9.94e-01 0.995
3 TrumpMargin 2.21e-07 0.028 1.10e-06 0.113
4 Running2022 3.11e-01 0.867 5.19e-01 0.995
5 NotRetiring 1.36e-01 0.247 3.40e-01 0.495
According to this analysis, the only variable worth considering is
TrumpMargin. It’s understandable: Trumpy voters elect Trump, and also elect
Trumpy senators who will defend Trump. Not very satisfying, but understandable.
(And I don’t understand why PartyRepublican wasn’t a good predictor?! Might
be something wrong there…)
Machine learning: supervised classification
It might be that the other features taken together will predict a bit more, so let’s move on to multivariate model. Here we’ll be using the redoubtable glmnet package [12], which will handle the multivarite logistic regression, LASSO regulation to impose an L1 penalty on model complexity (“choose the simplest model that’s adequately predictive”) and 3-fold crossvalidation to estimate out-of-sample predictivity.
Here’s how that works in broad, schematic outline:
- Crossvalidation: We divide the data into three subsets called “folds”, making sure everything is equitably divided among them. Each fold has the same number of Democrats & Republicans, the same Guilty and Not Guilty votes, the same number of Republican Guilty votes, and so on.
- Training vs test datasets: The we train a logistic regression model on 2 of the 3 folds (the training data), and estimate its performance by running it on the witheld fold (the test data). We do that for all combinations of training/test data subsets.
- Multivariate logistic regression: Ostensibly, we’re training a 6-parameter predictive model for the log odds ratio of a guilty vote (1 inhomogeneous offset $\beta_0$ + 5 predictor variables $\beta_i$).
- LASSO regularization: However, using all 5 predictors might overspecify the model, when a simpler subset of the predictors would do better out-of-sample. So glmnet uses the LASSO penalty, which imposes an L1 norm penalty on the number of variables used. Basically, you only get to add a variable if it does enough good for you, in terms of crossvalidated predictions made correctly. It will choose, for each crossvalidation round, the model that performs best and is simplest.
(There’s a lot more to know, but those are the high points.)
We then get a model which performs reasonably on the witheld test data, and which has the smallest number of parameters that is reasonably plausible. (Hastie adds a heuristic: find the best-predicting model, then choose an even simpler model whose crossvalidated error rate is within 1 standard error of the optimum. I.e., choose the simplest thing that’s statistically indistinguishable from the best. We won’t be bothering with that, for reasons you’ll see below.)
So let’s see what we can get!
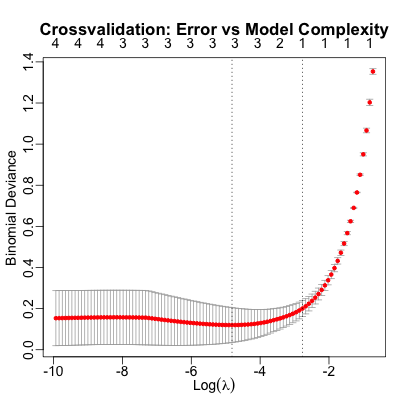 This shows the error in the predictions made (“binomial deviance”) as a function of model
complexity. The numbers along the top show the number of variables used in making the
prediction, with the simpler models on the right. The error bars around the red dots show
the variation across the rounds of crossvalidation. The 2 vertical dotted lines show the
best-predicting model, and Hastie’s simpler but statistically indistinguishable from best
heuristic.
This shows the error in the predictions made (“binomial deviance”) as a function of model
complexity. The numbers along the top show the number of variables used in making the
prediction, with the simpler models on the right. The error bars around the red dots show
the variation across the rounds of crossvalidation. The 2 vertical dotted lines show the
best-predicting model, and Hastie’s simpler but statistically indistinguishable from best
heuristic.
The best model uses 3 variables to predict the final verdict vote: the constitutionality
vote, the Trump margin in a senator’s state, and whether the senator is retiring.
Intriguingly, while TrumpMargin is the best single predictor, it is eclipsed
by the other 2 in a multivariate model:
1
(Intercept) -6.65610938
PartyRepublican .
VotedUnconst 8.21255164
TrumpMargin 0.03186794
Running2022 .
NotRetiring 1.96220073
The simpler model chosen by the Hastie heuristic uses the constitutionality vote alone.
The performance of the best model is pretty good. Here is a crosstabulation of the predicted votes (along the rows) and the actual votes (along the columns):
Actual
Predicted FALSE TRUE Total
FALSE 56 0 56
TRUE 1 43 44
Total 57 43 100
Percent Correct: 0.99
99% correct means we missed only 1 senator’s vote. A bit of digging reveals that it was Burr, who changed his mind between the constitutionality vote and the verdict vote.
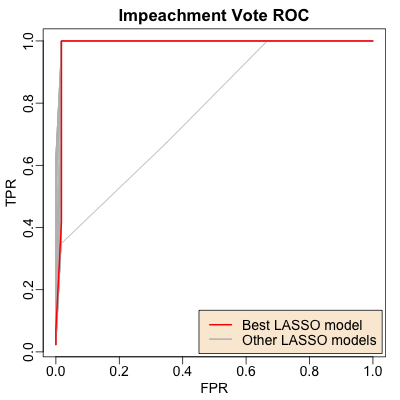
Finally, the Receiver Operating Characteristic curve (ROC curve) here shows the True Positive rate vs the False Positive Rate. The red curve is for the best model, and the gray curves are for the other models tested with different subsets of predictors. Normally, we’d use this curve to set a threshold on $\Pr(\mathrm{Guilty})$ to make an actual up-or-down Guilty prediction, so we could understand the tradeoffs between True Postive Rates (don’t miss any Guilty votes) vs False Positive Rate (don’t over-predict Guilty votes). But as you can see here, it’s near-perfect: party identity as expressed in the constitutionality vote predicts all. (Except, of course, Burr. Bless his little heart.)
Thinking about the results
 So what does it all mean?!
So what does it all mean?!
I was hoping for some kind of deep understanding of the pressures on senators: Trumpy constituents, reelection schedules, retirements, party identity, and so on. But it turns out those are all pretty correlated, and we have just a story about party identity:
- Trumpy voters elect Trump.
- Trumpy voters also elect senators who defend Trump.
There’s probably not much more here than that. We took a long time to find such a simple thing, no? As James Branch Cabell described the work of a bizarre bard in Music from Behind the Moon, one of the best short stories I’ve ever read, our song “ran confusedly, shuddering to an uncertain end”. [13]
But at least we know that the root of all evil here is the right-wing authoritarianism of the Trump crowd. Altemeyer’s exceptional book [14] summarizing his research career on right-wing authoritarianism is looking better each year in terms of its explanatory power, and more chilling each year.
Notes & References
1: B Booker, “Trump Impeachment Trial Verdict: How Senators Voted”, NPR, 2021-Feb-13.↩
2: United States Senate, “Vote Number 59: Guilty or Not Guilty (Article of Impeachment Against Former President Donald John Trump)”, Roll Call Vote 117th Congress – 1st Session, 2021-Feb-13. ↩
3: United States Senate, “Vote Number 57: On the Motion (Is Former President Donald John Trump Subject to a Court of Impeachment for Acts Committed While President?)”, Roll Call Vote 117th Congress – 1st Session, 2021-Feb-09.↩
4: Wikipedia, “2020 United States presidential election (results by state)”, retrieved 2021-Feb-15. ↩
5: United States Senate, “Class I – Senators Whose Term of Service Expire in 2025”, Qualification & Terms of Service, 2021-Feb-13. ↩
6: United States Senate, “Class II – Senators Whose Term of Service Expire in 2027”, Qualification & Terms of Service, 2021-Feb-13. ↩
7: United States Senate, “Class III – Senators Whose Term of Service Expire in 2023”, Qualification & Terms of Service, 2021-Feb-13. ↩
8: N Rakich & G Skelley, “What All Those GOP Retirements Mean For The 2022 Senate Map”, FiveThirtyEight, 2021-Jan-25. ↩
9: A Rogers, M Raju, & Ted Barrett, “Retirements shake up 2022 map as Republican senators eye exits”, CNN, 2021-Jan-26. ↩
10: Weekend Editor, “R script for Republican impeachment vote analysis”, SomeWeekendReading blog, 2021-Feb-24. There is also a text transcript of running this script, to verify the results reported here.↩
11: Weekend Editor, “Omnibus dataset for 2021 senate impeachment votes”, SomeWeekendReading blog, 2021-Feb-24.↩
12: J Friedman, T Hastie, R Tibshirani, “Regularization Paths for Generalized Linear Models via Coordinate Descent”, Journal of Statistical Software, 2010 33(1), 1–22.↩
13: J B Cabell, Music from Behind the Moon: An Epitome, 1926.↩
14: B Altemeyer, The Authoritarians, The Authoritarians web site, 2006.↩

Gestae Commentaria
Comments for this post are closed pending repair of the comment system, but the Email/Twitter/Mastodon icons at page-top always work.