Mea Culpa: Efficacies Don't Average!
Tagged:COVID
/
Math
/
MathInTheNews
/
MeaCulpa
/
PharmaAndBiotech
/
Statistics
A couple days ago, commenting at TheZvi, I blithely averaged efficacies from the early and late cohorts of the molnupiravir trial. Fellow commenter Thomas pointed out that this is not correct! This post is a mea culpa and a lesson to myself on How to Do It Right.
What’s the sitch?
During the FDA hearing on molnupiravir, it became apparent that:
- The interim analysis of the early cohort of patients showed fantastic efficacy vs hospitalization: 48.3% (CL: 20.5% – 66.5%).
- The final analysis of the full cohort showed “meh” efficacy: 30.4% (CL: 1.0% – 51.1%).
I was opining that in order to come down from ~50% to ~30%, the second cohort of the trial must have been pretty miserable! Just winging it, I thought:
- Suppose the interim and “completion” cohort are about the same size.
- Then the efficacy of the whole trial should be about the average of the interim and completion cohorts.
- So the efficacy of the late cohort must have been about 10%: (50% + 10%) / 2 = 30%.
The point I was trying to make was that the second cohort of the trial had to be really miserable in order to drag down the overall result like that.
Fellow commenter Thomas pointed out that this averaging business is oh-so-wrong: efficacies do not average like that! So, Thomas: warm thanks to you, for pointing that out. I do know how to do this calculation, but I needed the reminder not to make cavalier guesses. I owe you a favor for this.
So the point of this post is (a) to own my mistake and learn from it, and (b) to get archived here for myself (and anybody else who cares) How to Do It Right.
Let’s do it right
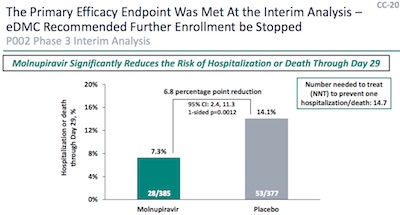
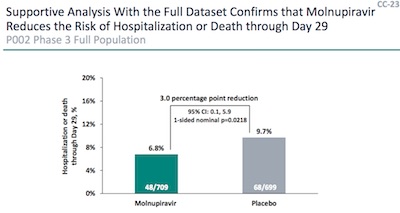 When we
blogged the FDA molnupiravir hearings,
we picked up slides CC-20 and CC-23 from the Merck deck [1],
shown here. They contain what we need: patient and hospitalization counts, for the
control and treatment arms, for the interim and full analysis. Subtracting the interim
counts from the full counts will give us the counts for the “completion” set, i.e., the
rest of the patients. [2]
When we
blogged the FDA molnupiravir hearings,
we picked up slides CC-20 and CC-23 from the Merck deck [1],
shown here. They contain what we need: patient and hospitalization counts, for the
control and treatment arms, for the interim and full analysis. Subtracting the interim
counts from the full counts will give us the counts for the “completion” set, i.e., the
rest of the patients. [2]
Let $N_x$ be the number of patients in an arm ($x = $ treatment or control), and let $K_{x\mbox{hosp}}$ be the number of those who go on to be hospitalized. So the 3rd row in this table is obtained by subtracting the second row from the first row:
| Cohort | $N_{\mbox{trt}}$ | $K_{\mbox{trthosp}}$ | $N_{\mbox{ctl}}$ | $K_{\mbox{ctlhosp}}$ | ||||
|---|---|---|---|---|---|---|---|---|
| Full | 709 | 48 | 699 | 68 | ||||
| Interim | 385 | 28 | 377 | 53 | ||||
| Completion | 324 | 20 | 322 | 15 |
For any arm, we can get a point estimate of the efficacy by:
\[\begin{align*} \mbox{Efficacy} &= 1 - \frac{\Pr(\mbox{infect} | \mbox{treated})}{\Pr(\mbox{infect} | \mbox{control})} \\ &= 1 - \frac{K_{\mbox{trthosp}} / N_{\mbox{trt}}}{K_{\mbox{ctlhosp}} / N_{\mbox{ctl}}} \end{align*}\]We can do a little more by getting 95% confidence limits, which as a retired statistician I am required to do, under international law. I wrote a little R script to do this [4], which really just uses scaled binomial confidence intervals:
library("gsDesign") # For ciBinomial()
efficacyAndCL <- function(Ntrt, Ktrt, Ncnt, Kcnt) { # Treatment efficacy & 95% conf limit
## Ntrt = number of subjects in treatment arm
## Ktrt = number of sick in treatment arm
## Ncnt = number of subjects in control arm
## Kcnt = number of sick in control arm
eff <- 1 - (Ktrt / Ntrt) / (Kcnt / Ncnt) # Point estimate, then confidence limits
effCL <- rev(1 - ciBinomial(Ktrt, Kcnt, Ntrt, Ncnt, scale = "RR"))
c(LCL = effCL[[1]], Eff = eff, UCL = effCL[[2]]) # Return 3-vector of LCL, estimate, and UCL
} #
(I’d prefer to use my new Bayesian method of the distribution of Beta-distributed variables, but I haven’t finished the tricky numerics of ${}_{3}F_{2}()$ for large parameter values.)
So let’s see what we get:
## Full cohort
> round(efficacyAndCL(709, 48, 699, 68), digits = 3)
LCL Eff UCL
0.010 0.304 0.511
## Interim cohort
> round(efficacyAndCL(385, 28, 377, 53), digits = 3)
LCL Eff UCL
0.204 0.483 0.665
## Completion cohort
> round(efficacyAndCL(324, 20, 322, 15), digits = 3)
LCL Eff UCL
-1.516 -0.325 0.301
So, in table form and expressed as percentages, we get:
| Cohort | 95% LCL | Efficacy | 95% UCL | |||
|---|---|---|---|---|---|---|
| Full | 1.0% | 30.4% | 51.1% | |||
| Interim | 20.4% | 48.3% | 66.5% | |||
| Completion | -151.6% | -32.5% | 30.1% |
Yeah… that second half of the trial, shown in bold, looks like it was pretty miserable! The efficacy is negative, meaning there were more hospitalizations in the treatment arm than in the control arm (20 vs 15). Those are pretty small numbers though, and hence the 95% confidence limits are quite wide.
It should be clear now why the FDA AMDAC chair, Lindsey Baden, described the efficacy as “wobbly”.
The Weekend Conclusion
Ok, I learned 2 things here:
- I was wrong to average efficacies in order to conclude that the completion cohort was low performance. Many thanks to Thomas for correcting me, thereby giving me this opportunity to clear up my thinking here.
- The completion cohort really was miserable, more so even than I thought.
Every mistake is an opportunity to learn better.
Notes & References
1: S Curtis, D Hazuda, K Blanchard, N Karsonis, “Molnupiravir: U.S. Food & Drug Administration Antimicrobial Drugs Advisory Committee November 30, 2021”, FDA AMDAC 2021-Nov-30 Materials, retrieved 2021-Nov-30. ↩
2: Approximately! To do this completely correctly, we’d have to have the censoring data, i.e., when patients dropped out of the trial, and use some method related to Cox regression to handle that.
However, consulting the Merck submission document [3, p. 46], we see that the treatment arm shrank by 385 - 357 = 28 dropouts, and the control arm shrank by 377 - 324 = 53 dropouts. So that’s a total dropout rate of:
\[100\% \times \frac{28 + 53}{385 + 377} = 10.6\%\]So while it’s wrong to ignore this, it might not be excessively misleading because of the low-to-moderate dropout rate. But you would be right to be suspicous of anybody who did what I’m about to do if they had access to the censorship data!↩
3: Merck Staff, “Center for Drug Evaluation and Research, Antimicrobial Drugs Advisory Committee Meeting Briefing Document: Molnupiravir, Oral Treatment of COVID-19, APPLICATION NUMBER: EUA #000108”, FDA AMDAC 2021-Nov-30 Materials, retrieved 2021-Nov-30. There is also a 7-page addendum. ↩
4: Weekend Editor, “R script for efficacy confidence limits by scaled binomial ratio”, Some Weekend Reading blog, 2021-Nov-12. ↩

Gestae Commentaria
Comments for this post are closed pending repair of the comment system, but the Email/Twitter/Mastodon icons at page-top always work.