On New COVID-19 Therapeutics

Vaccines are great, but now there are some exciting new treatments for COVID-19, in case you get a breakthrough infection (or made the wrong choice about accepting vaccination). Let’s look at how well they work, and what they might cost in comparison to other things.

A quick review of efficacy percentage and its confidence limits

We talk about efficacy of a vaccine or other treatment, as a number telling how much the risk of infection, hospitalization, or death is reduced, compared to the untreated popultion. In other words:

• Efficacy of 100% means nobody in the treatment arm of a trial got sick.
• Efficacy of a positive percent means the treatment helped, i.e., the treatment arm got sick somewhat less often than the untreated arm.
• Efficacy of 0% means the treated & untreated people got sick at about the same rate, i.e., treatment didn’t help and didn’t hurt.
• A negative efficacy means the treated subjects got sick more often than the untreated, i.e., the treatment is actively harmful.

So that’s just a ratio of 2 probabilities and a little arithmetic. You can calculate it yourself on paper if you can learn just 4 integers: the number of subjects in the treatment & control arms ($N_{\mbox{trt}}$, $N_{\mbox{cnt}}$) and the number in each arm who got sick ($K_{\mbox{trt}}$, $K_{\mbox{cnt}}$).

But that’s not quite the end of the story. Of course we’re estimating the probabilities here, by examining a finite number of patients. That means the efficacy is itself a random variable, which has some distribution due to measurement uncertainty and sample size. So we’d like also to know the 95% confidence limits (CL): what’s the lowest and highest it can be, such that we’re 95% confident the true value is inbetween? The lower confidence limit (LCL) is the 2.5% quantile, and the upper confidence limit (UCL) is the 97.5% quantile.

There are lots of ways of computing this, depending on how much modeling you want to do. My favorite, which I haven’t finished working on yet, involves the ratio of Beta-distributed variables as captured by a Gauss hypergeometric function ${}_2F_1()$.

But until that’s working, I’ll use some other methods in the R package gsDesign. The function ciBinomial() is all about confidence intervals involving binomially-distributed variables. You can see how the probabilities in the efficacy equation above can be viewed as scaled binomial variables (using the arm size as the scale). By telling ciBinomial() we want a risk ratio, we’ll get confidence limits on the efficacy.

We’ve packaged that up in a nice little script ^[1], which basically does:

rev(1 - ciBinomial(Ktrt, Kcnt, Ntrt, Ncnt, scale = "RR"))

to get the confidence limits.

New COVID-19 therapeutics

Vaccines are great. Really, really great. Preventing disease is always better than treating it.

But… disease happens. There are (rare) breakthrough COVID-19 infections in the vacccinatd, and (regrettably not rare) people who won’t get vaccinated. We’d like to be able to take good care of them, too.

Today we’ll look at treatment efficacy for 2 new COVID-19 therapeutics:

1. At the beginning of October, Merck’s study on molnupiravir debuted with much fanfare. ^[2] It’s a pseudo nucleotide, which the virus will incorprate in its RNA when it’s replicating. That causes hypermutation and catastrophic failure. Clever, really. We previously analyzed their result on this crummy little blog that nobody reads, and it was pretty good!
2. Just last week, Pfizer announced that the trial on paxlovid was stopped, because the trial results were so good! ^[3] It’s a protease inhibitor, part of a large family of drugs that interrupt the functioning of some viral proteins in proteolysis. This is the family of drugs that have revolutionized the treatment of HIV and hepatitis-C. They’re not super expensive to make, they have a pretty well understood safety profile, and they can be taken chronically. So that’s pretty good news.

Let’s look at their efficacy numbers.

For molnupiravir, the total number of subjects and the number of hospitalizations in each arm of the trial were, as we determined approximately in a previous post:

> mnpData <- matrix(c(53, 28, round(53/0.141), round(28/0.073)), nrow = 2, ncol = 2, byrow = FALSE,
                    dimnames = list(c("Placebo", "Treatment"), c("Ncases", "Ntotal"))); mnpData
          Ncases Ntotal
Placebo       53    376
Treatment     28    384

So we calculate the efficacy vs hospitalization at 48.3% (CL: 20.5% – 66.5%):

> signif(efficacyAndCL(384, 28, 376, 53), digits = 3)
  LCL   Eff   UCL
0.205 0.483 0.665

For paxlovid, the numbers are a trial of very similar size, as reported in the WaPo ^[4]:

> paxData <- matrix(c(27, 3, 385, 389), nrow = 2, ncol = 2, byrow = FALSE,
                    dimnames = list(c("Placebo", "Treatment"), c("Ncases", "Ntotal"))); paxData
          Ncases Ntotal
Placebo       27    385
Treatment      3    389

So we calculate the efficacy vs hospitalization at 89.0% (CL: 66.3% – 96.4%):

> signif(efficacyAndCL(389, 3, 385, 27), digits = 3)
  LCL   Eff   UCL
0.663 0.890 0.964

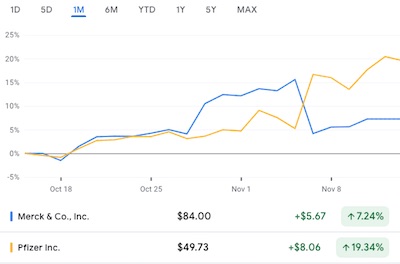That’s even better than molnupiravir: the lower confidence limit of paxlovid (worst case) is about the same as the upper confidence limit (best case) for molnupiravir.

Look at what happened to the relative prices of Merck and Pfizer when this was announced last week. People aren’t stupid about this.

Both drugs are going to be good, and probably even better if used in combination, perhaps along with fluvoxamine. But paxlovid looks better for now, if you can only get one of them.

Why that matters

• Cost: Merck seems to have priced a course of molnupiravir at $700, which seems pretty reasonable. Pfizer hasn’t priced paxlovid yet, but other protease inhibitors aren’t super expensive. I dug a little bit to get pricing on other COVID-19 treatments, and by comparison they’re much more expensive:
  • Regeneron’s mab cocktail (casirivimab and imdevimab): $1250 per infusion, plus cost of skilled nursing care to do it and a facility in which to do it.
  • GSK & Vir’s mab cocktail (sotrovimab): about $2100 per infusion, plus skilled nursing and facility charges.
  • Remdesivir: about $3120 for a course of treatment.
• Administration: These are oral: just a pill you take. The antibody infusions you have to go to a clinic and get an IV line put in, and sit there for maybe an hour. It’s just easier on patients, and they take the pill at home where they won’t load up the medical system.
• Synergy: I used to do a lot of synergy research in oncology, where therapies get combined to deliver a stronger effect than either drug alone. Since molnupiravir and paxlovid work by completely different mechanisms of action, it would be interesting to see if there were synergy in using both simultaneously. Or better yet, a 3-way combination of molnupiravir, paxlovid, and fluvoxamine? Or in combination with the antibody therapies, because why not check?
• Safety: Paxlovid, at least, is in a class of drugs that have been well-used for 25 or so years, so we know a lot about their safety. People with HIV take them chronically, daily for years and years.
• Prophylaxis: If you test positive for COVID-19, what can we do for your contacts other than test them? Both molnupiravir and paxlovid have to be given early. Can we give them as a preventive, before people start showing symptoms? It would be great if we could offer them as a therapy to people found in contact tracing, and might even be able to stop outbreaks in their tracks.

That’s an awful lot of powerfully positive protective mana barreling down the road at us.

The Weekend Conclusion

We can prevent COVID-19 with vaccines (though we do need to learn how to persuade people to get vaccinated). Now we can treat COVID-19 if caught early enough, with at least 2 new drugs, in addition to the antibody infusions, dexamethasone, and so on.

Things are slowly getting better.

Addendum 2021-Nov-14: Death rates in the paxlovid trial

After some discussion in the comments over at TheZvi’s blog, we should also examine the death rates in the paxlovid trial.

The confusing thing here is that there were 0 deaths in the paxlovid arm vs 7 deaths in the control arm. That seems to lead to an efficacy vs death of 100%… which, understandably, people have trouble swallowing.

> paxDataD <- matrix(c(7, 0, 385, 389), nrow = 2, ncol = 2, byrow = FALSE,
                     dimnames = list(c("Placebo", "Treatment"), c("Ndead", "Ntotal"))); paxDataD
          Ndead Ntotal
Placebo       7    385
Treatment     0    389

> signif(efficacyAndCL(389, 0, 385, 7), digits = 3)
  LCL  Eff  UCL
 0.46 1.00 1.00

Here’s how I would have reported it: yes, the efficacy vs death was measured at 100% (CL: 46% – 100%).

But with a 95% confidence limit of 46% – 100%?! From a Bayesian point of view, that very broad confidence interval (technically Bayesians would call it a “credibility interval”) means the posterior distribution of the efficacy is very, very wide. It is your warning that the trial isn’t really powered to report on the blessedly rare event of death. A very cautious person might conclude that death rates were reduced by at least 46%, probably more, maybe as much as 100%… but we can’t say with confidence exactly how much more.

Still, a worst case 46% reduction in death is a good result!

Notes & References

1: Weekend Editor, “R script for efficacy confidence limits by scaled binomial ratio”, Some Weekend Reading blog, 2021-Nov-12. ↩

2: M Herper, “Merck’s antiviral pill reduces hospitalization of Covid patients, a possible game-changer for treatment”, STAT News, 2021-Oct-01. ↩

3: M Herper, “Experimental Pfizer pill prevents Covid hospitalizations and deaths”, STAT News, 2021-Nov-05. ↩

4: CY Johnson, “Antiviral pills from Pfizer, Merck, show promise against worst covid-19 outcomes”, Washington Post, 2021-Nov-05. ↩