AstraZeneca/Oxford vaccine interim readout (and its discontents)

Somebody asked me about the early readout this week of the AstraZeneca/Oxford vaccine Phase 3 trial. Initially they said 70% efficacy. It’s not a stunningly good 95% result like Pfizer or Moderna; still, it’s a good, craftsmanlike bit of work. But then… things got weird.

Yet another round of science by press release – here at Chez Weekend we understand the tight schedule constraints & are prepared to be reasonably sympathetic. But we are getting a bit testy at having to comb through the vague, blurred, and ambiguous pronouncements of managers, lawyers, and PR people instead of scientific evidence. In the recent cases of Pfizer and Moderna, this seems to have worked out mostly ok.

But not this time.

How the AZ/OX vaccine works (vastly oversimplified)

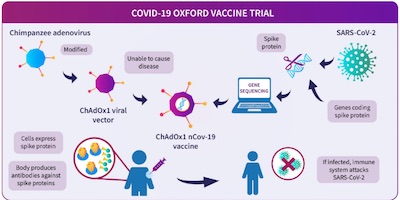Recall that the AZ/OX vaccine is much more complex. It uses a viral vector: they take an existing virus capable of infecting humans, scoop out its genetic material using a mind-bendingly complex and careful process, then give it the genetic material of only the SARS-COV-2 virus spike protein. This little chimeric monster is capable of infecting exactly 1 cell, 1 time, using the protein envelope of the vector virus. That causes the SARS-COV-2 spike protein to be made in some quantity in the infected cell. Your immune system, theoretically, then reacts to the spike protein and produces immunity.

The point of the viral vector is to have a protein envelope which (a) preserves the mRNA in your blood long enough to do something, since bare mRNA is quickly degraded, and (b) gain entry to 1 cell per virus. Pfizer, Moderna, and even Sanofi have a lipid nanocapsule technology that does this without having to use an existing vector virus.

But… if you use an existing human virus, some of your population will already be immune to it (like cold viruses: old people have had a lot of colds). So they used a simian adenovirus, ChAdOx1 (basically monkey colds). Unless you live in close proximity to chimps and somehow exchange nasal fluids with them, you probably aren’t immune to this one. ^[1]

There are a few other differences, like changing an amino acid to stabilize the spike protein and replacing thei viral leader sequence with human TPA. These appear to be engineering concessions to pragmatism, and look pretty reasonable.

But the simian adenovirus will, sort of, infect human cells. So… maybe it’ll work?

The AZ/OX press releases

First up is the press release from AstraZeneca, and the Oxford version. ^{[2] [3]} They claim 70% efficacy, which is actually pretty good, albeit not quite like the 95% efficacies seen by Pfizer & Moderna. But… there were 2 dosing regimens (and controls):

• One group got a full dose initially, and a full dose in the second booster. This group had a 62% efficacy rate ($N = 8895$).
• The other group got a half dose initially, and a full dose on the second booster. This group had a 90% efficacy rate ($N = 2741$).

Combining these 2 groups – somehow ^[4] – is claimed to have an efficacy of 70%.

One nice thing is that people in the control arm didn’t just get an injection of saline, they got a meningococcal vaccine MenACWY on the first dose, and saline on the second. Assuming they haven’t had MenACWY (or a meningococcus infection), they’ll have some reaction to the first dose and thus won’t know they’re in the control arm. Good for AstraZeneca! (But… apparently the subjects at the Brazilian sites got saline?!)

But (again)… the smell of the rest of the press release immediately raises questions:

• Why are they doing multiple doses? You’re supposed to know the dose by the time you start Phase 3. That’s what Phases 1 & 2 are for: to test safety and find a dose, along with any efficacy you can pick up along the way. The press release is silent about why this might be: is it a clever design or an error?
• Why is the high efficacy response in the low dose group? Normally you like to see the efficacy be dose-responsive, i.e., increase along with the dose (though there are some exceptions, which are called instances of hormesis). There could be a thousand reasons (see below), but the press release just glosses over this like it’s No Big Deal.
• Why do the different dose groups have different age cutoffs? The press release does not admit this, which is a serious breach of truth-telling. It says COV002 and COV003 both require ages 18 or older. But if you dig a little deeper, you find that the lower-dose arm had an upper age cutoff of 55 (so no elders) while the other did not (and had elders enrolled). This means the dose difference is hopelessly convolved with the age of the test population! Also, the way this was designed, one population was in Brazil and the other in the UK, so local habits of living are also convolved with dose.

That sobbing sound you hear in the background is statisticians all over the world, gently weeping.

Ok, we gotta dig deeper!

Why does the lower dose get higher efficacy?

Our next 2 stops are Derek Lowe’s blog In the Pipeline at Science Translational Medicine ^[5], and a news article at Nature by Ewen Callaway.^[6] Both posit similar mechanisms to explain why the lower dose had the higher efficacy:

• Immune systems are highly complex and nonlinear, so maybe there’s a feedback mechanism to throttle down T cell reactionsn to the high dose?
• Maybe a high initial dose also induced an immune reaction against the viral vector, so those patients were primed to resist the second dose?
• Maybe there were a lot of asymptomatic but infected people in the trial, who would then, according to the trial protocol, be excluded from the endpoint?
• Crazily, one dose arm included elders while the other did not! Isn’t that a good reason to expect different effiacies?

In some ways, this is satisfyingly perverse: biology is just maddening in the way that everything interacts with everything else, all the time. This is the sort of roadblock you’d expect… but why didn’t the Phase 1/2 dose finding trials find this?

Now the story takes a slightly darker turn, for 2 reasons:

1. Nowhere in the AZ/OX press releases did they mention that the low dose group had an age cap of 55, while the high dose group did not. It would be madness to design a trial this way, and we only find out about it through other sources. In this case, it comes to us from Moncef Slaoui, the head of Operation Warp Speed. ^[7] So the efficacy difference is hopelessly entangled with age differences in the test populations.
2. It turns out the 2 doses in a Phase 3 trial were not some clever thing, but a blunder in manufacturing and delivery: an accident. ^{[8] [9] [10]} Apparently, when this was discovered, AZ & OX went to the regulatory authorities (FDA, EMA, … and whatever the Brazilian equivalent is) and disclosed this. Good for them; that’s the right thing to do. The regulatory bodies said to continue as if it had been designed as a 2-dose vs placebo trial, which is about as much as you can do to salvage the situation.

However, the data are now pretty weird. Kirka’s article ^[10] quotes David Salisbury, an associate fellow of the global health program at Chatham House:

“You’ve taken two studies for which different doses were used and come up with a composite that doesn’t represent either of the doses,” he said of the figure. “I think many people are having trouble with that.”

Indeed!

The Bottom Line(s)

There are 2 bottom lines that I see here:

1. We don’t really know the efficacy. One simply cannot average different doses given to different age populations living in different countries!
2. There is now a trust gap. Neither AstraZeneca nor Oxford mentioned in their press releases that the multi-dose design was the result of an error, nor did they admit the efficacy difference could be partially explained by younger test subjects.

This is the problem with science by press release: the PR is always wordsmithed by PR people, managers, and lawyers to give it “good spin”, sometimes (I hope inadvertently) at the expense of truth. I’d be much more understanding if the initial PR had said, “Hey, we kind screwed up a few things, but the underlying efficacies are still pretty good some of the time.” But they chose instead to tell just part of the truth.

Both Pfizer/BioNTech and Moderna/Lonza were pretty convincing. AZ/OX… not so much. As of yesterday, the AstraZeneca CEO is admitting they might have to do another Phase 3 clinical trial to clean up the mess. ^[11]

Sounds about right.

Added 2020-Dec-01

A little birdie whispered in my ear that, based on the Lancet publication of the Phase 2/3 COV002 (UK) trial, AZ/OX had the doses for their trial sites manufactured by 2 different CMOs.

A Contract Manufacturing Organization (CMO) will make small to medium-sized batches of medications for you, to your specifications, under GMP guidelines. (GMP means Good Manufacturing Practice, i.e., survivable under FDA auditors.) This makes sense if you don’t have your large-scale manufacturing line up and going yet. In exchange for only somewhat disturbingly large piles of money, you can get enough to run your trial now, rather than later. Thus in the case of a pandemic, being early to market means fewer people die. In more pedestrian cases, it means earlier market entry, with all the revenue and first-mover advantage implied.

It’s a defensible thing for AZ/OX to have done.

But… COBRA Biologics supplied the drug for the 18-55 year old cohort, and Advent supplied the doses for all the rest. COBRA apparently messed up and made the first batch at half strength.

That explains the source of the half-dose blunder. It does not explain other blunders:

• Why didn’t they assay a random sample from each CMO’s batch of doses? Just a little in-house QC to make sure they had what they thought they had could have saved a world of grief!
• Why didn’t they randomize the CMO batches between cohorts? One of the things that regularly made me tear my hair out in frustration was that some of my experimentalist colleagues would resist randomization. “Too much work”, they would say… and then it was somehow my fault when their treatment effect was hopelessly tangled up with batch effects. C’mon, this is basic; that’s why they call it a randomized clinical trial. You randomly assign patients (from the same age cohort!) to treatment vs control arms, you randomly assign batches to trial sites, you keep the trial at least double-blind (the patient doesn’t know what they’re getting, the doc doesn’t know what he’s injecting, only the bar codes are recorded and then unblinded at the end).
• Why did some cohorts have a 55 year old age cap, while others did not? Of course the younger cohort responds better! But now it’s all convolved with dose levels, so you can’t tell what’s going on.
• Why didn’t this come out in their press release, but only after persistent digging? Getting the whole truth out early is fundamental to establishing trust.

So it’s a bit more understandable… but no prettier. The AZ/OX vaccine probably works… but we won’t know until there’s another trial.

Notes & References

1: And if you do regularly exchange nasal fluids with monkeys, I don’t want to hear about it. Go make your own Monkey Snot Blog, not here. ↩

2: AstraZeneca, “AZD1222 vaccine met primary efficacy endpoint in preventing COVID-19”, AstraZeneca press releases, 2020-Nov-23. ↩

3: Oxford Univesity, “Oxford University breakthrough on global COVID-19 vaccine”, Oxford University News & Events, 2020-Nov-23. ↩

4: The method used must involve Cox regression/Kaplan-Meier curves, for which the data was not released. Naïve combination methods don’t match the result:

> (62+90)/2
[1] 76
> (62*8895 + 90*2741) / (8895 + 2741)
[1] 68.59574

↩

5: D Lowe, “Oxford/AZ Vaccine Efficacy Data”, In the Pipeline at Science Translational Medicine, 2020-Nov-23. ↩

6: E Callaway, “Why Oxford’s positive COVID vaccine results are puzzling scientists”, Nature, 2020-Nov-23. ↩

7: J Lauerman & A LaVito, “Astra Vaccine’s 90% Efficacy in Covid Came in Younger Group”, Bloomberg, 2020-Nov-24. ↩

8: L Burger & K Kelland, “Dosing error turns into lucky punch for AstraZeneca and Oxford”, Reuters, 2020-Nov-23. NB: They can still call it “lucky”, since the different age caps were not revealed until the next day, and the efficacy difference could still be called “serendipity”. ↩

9: J Paton & S Ring, “AstraZeneca Faces More Vaccine Questions After Manufacturing Error”, Bloomberg, 2020-Nov-26. ↩

10: D Kirka, “AstraZeneca manufacturing error clouds vaccine study results”, MedicalXPress, 2020-Nov-25. ↩

11: S Ring & J Paton, “Astra Eyes Extra Global Vaccine Trial as Questions Mount”, Bloomberg, 2020-Nov-26. NB: It appears the AZ CEO still insists the manufacturing/delivery error was “not a mistake” because they amended the trial protocol to accomodate it. A rigid insistence on being always right does not inspire confidence, at least not from me. ↩