The Weekend Editrix Exposed to COVID-19: An Adventure with Bayes Rule in Medical Testing

Last weekend, the Weekend Editrix was exposed to a person who tested positive for COVID-19. The need for rapid testing suddenly became very real for us. While waiting for the test to work, we worked out the Bayesian stats for the test: a positive test means near-100% chance of COVID-19, while a negative test means 89.4% chance of no COVID-19.

What’s the sitch?

We are members of a religious community.

For most of 2020, meetings were quickly transitioned to Zoom, like everything else. Some things worked surprisingly well, and others… not so much. Humans are to some degree social creatures, and in a religious context we often crave the emotions associated with social contact.

So once vaccines were rolled out sufficiently well, we reconvened in person — though vaccinated, masked, socially distanced, and with hand sanitizer everywhere. We also reported (respecting medical privacy) any COVID-19 contacts that might have happened, so people would know when to test. That seemed to work pretty well.

But we learned this afternoon from our religious community that the Weekend Editrix was exposed last weekend. (Your humble Weekend Editor, being laid up with a back injury, participated via Zoom. Any exposure to me would be through the Weekend Editrix.) Suddenly, we were very interested in the availability, price, speed, and accuracy of home COVID-19 test kits, to decide what to do next. This is especially so since the Weekend Editrix works with a social service agency that visits elder care facilities, and we absolutely do not want to inject COVID-19 there!

Rapid antigen test kits

Fortunately, a quick call to our local pharmacy revealed they had several kinds of test kits. But… about 30min later when we arrived, they had only 1 kind of test kit and only 3 of them: the ACON Laboratories Flowflex COVID-19 Antigen Home Test kit, authorized by the FDA on October 4th. ^[1]

Here’s what the FDA said about approving this test:

This action highlights our continued commitment to increasing the availability of appropriately accurate and reliable OTC tests to meet public health needs and increase access to testing for consumers.

“Accurate” means it tells you the truth; “reliable” means it keeps telling you the truth if you test over and over again. Sounds good to me.

It was frustrating that the pharmacy phone call claimed abundance and diversity of tests, but very quickly that situation turned into just a few of exactly 1 kind of test. And, of course this being the United States, they were not free. Limited variety, limited availability, and then only if you can pay.

With a sigh, we paid. It wasn’t a lot at all by our standards, but if we had been poor, or students, or just really desperate, it could have been bad. Especially with therapeutics like molnupiravir and paxlovid coming that only work in early days after symptoms: it will be crucial to have testing be universally available and free. We’re not there yet.

The test

Fortunately, the test was easy enough to operate that even a couple of older PhDs could do it without too much problem. After swabbing the Weekend Editrix’s nose, we used the buffer solution to extract the antigens into solution. We put the 4 required drops of loaded buffer into the sample chamber, and watched the sample strip gradually turn pink as the goop diffused along.

The readout is kind of interesting: there are 2 red bars that might appear, labelled “C” and “T” (photo below; spoiler alert).

• The C bar stands for “control”: it indicates whether the test is working, and must always show up or the test is broken. (If C doesn’t show up, you have to try again with another test kit.)
• The T bar stands for “test”: if it shows up, even faintly, then you’re likely infected. If it doesn’t show up, even faintly, then you’re likely not infected.

I wonder how much we should trust that; how much work is the word “likely” doing there? We had 15 minutes to think it over, while the test did its stuff.

So I read the box insert on the test. (Hey, sometimes reading the manual is The Right Thing, no?)

• It’s described as having a low False Positive Rate (FPR) by which most people understand: if it comes up positive you’ve almost certainly got COVID-19.
• It’s also said to have a somewhat higher False Negative Rate (FNR), by which most people understand: if it comes up negative then you might be in the clear, but there’s some chance you’re not.

“Most people understand” incorrectly.

As a cranky, grizzled old statistician this bothered me. Let’s work out the details while we’re waiting for the test, shall we?

For a binary test like this, there are 2 things going on:

• Reality: you either have COVID-19 (+) or you don’t (-).
• Test: the test either comes up positive (+) or negative (-).

These are not the same! The test can lie to you, hopefully with small probability. If you run the test on $N$ people, you come up with people divided among 4 cases:

• True Positives: $TP$ of them who have COVID-19 and test positive.
• True Negatives: $TN$ of them who do not have COVID-19 and test negative.
• False Positives: $FP$ of them who do not have COVID-19 but the test lies and gives a positive anyway.
• False Negatives: $FN$ of them wo do have COVID-19 but the test lies and gives a negative anyway.

Obviously that’s all the cases:

\[N = TP + TN + FP + FN\]

I mean, it’s just 4 integers. How hard can it be? (Never say this.)

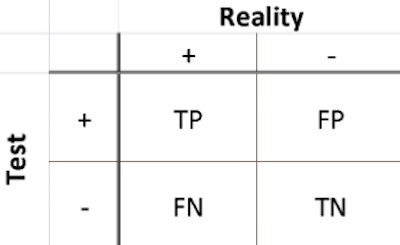These can be arranged in a table, as shown here. The test result (+/- for the test readout) is shown on the rows, but the unknown truth of the matter is shown on the columns (+/- for having COVID-19 or not). Obviously, you’d like that table to be diagonal: as near as you can get, $FN = 0$ and $FP = 0$ so that the test always tells you the truth.

If you’re the developer of the test, you try to engineer that. In fact, you try very hard! You run the test on samples of known COVID-19 status, and measure the Bayesian probability of the test lying either way, called the False Positive Rate and the False Negative Rate:

\[\begin{alignat*}{4} \mbox{FPR} &= \Pr(\mbox{Test+} | \mbox{Reality-}) &&= \frac{FP}{FP + TN} \\ \mbox{FNR} &= \Pr(\mbox{Test-} | \mbox{Reality+}) &&= \frac{FN}{FN + TP} \end{alignat*}\]

Usually people keep those 2 types of error separated, since there are different consequences of a false positive (somebody gets treated for a disease they don’t have, which is bad) and a false negative (somebody doesn’t get treated for a disease they do have, which is really bad). But if you wanted to, you could just lump them together into the stuff you get right and the stuff you get wrong (usually called the Misclassification Rate):

\[\begin{align*} \mbox{Fraction Right} &= \frac{TP + TN}{TP + TN + FP + FN} \\ \mbox{Misclassification Rate} &= \frac{FP + FN}{TP + TN + FP + FN} \end{align*}\]

So the developers at ACON Laboratories fiddled about with the test, trying to minimize the $\mbox{FNR}$ and $\mbox{FPR}$. Good for them. They did it well enough that the FDA approved their test last October. (Sheesh, why so long? More than a year and a half into a global pandemic?!)

But I’m not the test developer: I don’t care about optimizing their assay. I want to know if my spouse has COVID-19 or not! For that, we have other measures, some of which are the Bayesian duals of the above. Here are the 4 cases:

• Positive Predictive Value (PPV): If the test comes up positive, what’s the probability you have COVID-19?
• Negative Predictive Value (NPV): If the test comes up negative, what’s the probability you do not have COVID-19?
• False Discovery Rate (FDR): If the test comes up positive, what’s the probability the test lied and you’re actually still ok and do not have COVID-19? This is the Bayesian dual of the False Positive Rate above.
• Negative Overlooked Value (NOV): If the test comes up negative, what’s the probability the test lied and you really do have COVID-19? This is the Bayesian dual of the False Negative Rate above.

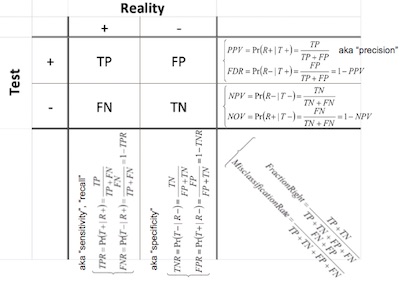We can annotate our little 2x2 table to show those as well, and you can see all the different ways to quantify error and correctness of a binary test. That’s what’s shown here (click to embiggen).

How about some concrete numbers? The package insert for the test said ^[2]:

Q: HOW ACCURATE IS THIS TEST?

A: The performance of Flowflex COVID-19 Antigen Home Test was established in an allcomers clinical study conducted between March 2021 and May 2021 with 172 nasal swabs self-collected or pair-collected by another study participant from 108 individual symptomatic patients (within 7 days of onset) suspected of COVID-19 and 64 asymptomatic patients. All subjects were screened for the presence or absence of COVID-19 symptoms within two weeks of study enrollment. The Flowflex COVID-19 Antigen Home Test was compared to an FDA authorized molecular SARS-CoV-2 test. The Flowflex COVID-19 Antigen Home Test correctly identified 93% of positive specimens and 100% of negative specimens.

So we know $N = 172$, with $S = TP + FN = 108$ (“S” for “sick”) presumed COVID-19 subjects and $H = TN + FP = 64$ (“H” for “healthy”) healthy subjects. We’ll interpret the quoted 93% and 100% as the True Positive Rate and True Negative Rate. So we have 4 equations in the 4 unknowns $TP$, $TN$, $FP$, $FN$:

\[\begin{align*} TP + FN &= S \\ TN + FP &= H \\ \mbox{TPR} &= \frac{TP}{TP + FN} \\ \mbox{TNR} &= \frac{TN}{TN + FP} \end{align*}\]

Pretty obviously, the solution is:

\[\begin{alignat*}{4} TP &= \mbox{TPR} \cdot S &&= 0.93 \times 108 &&= 100.44 \\ TN &= \mbox{TNR} \cdot H &&= 1.00 \times 64 &&= 64 \\ FN &= (1 - \mbox{TPR}) \cdot S &&= (1.00 - 0.93) \times 108 &&= 7.56 \\ FP &= (1 - \mbox{TNR}) \cdot H &&= (1.0 - 1.0) \times 64 &&= 0 \end{alignat*}\]

Now we’ve reconstructed the counts in the trial. Approximately: almost certainly we should round 100.44 to 100 and 7.56 to 8, because humans usually come in integer quantities (conjoined twins notwithstanding). That would amount to a TPR of 92.59% instead the 93% to which they sensibly rounded. Armed with that, we can compute the Positive Predictive Value and the Negative Predictive Value:

\[\begin{alignat*}{5} \mbox{PPV} &= \frac{TP}{TP + FP} &&= \frac{100.44}{100.44 + 0} &&= 100.0\% \\ \mbox{NPV} &= \frac{TN}{TN + FN} &&= \frac{64}{64 + 7.56} &&= 89.4\% \end{alignat*}\]

Result:

• If the test is positive: be 100% (ish) sure we have a COVID-19 case.
• If the test is negative: be 89.4% sure we do not have a COVID-19 case (which is pretty good, as these things go).

Grumble: Why couldn’t they just quote the PPV and NPV on the box, and not make me go through all that?! This is the sort of thing that makes a grizzled old statistician grumpy.

Now… how would one go about putting confidence limits on the PPV and NPV? Hmm…

Ding! The kitchen timer went off. No time for confidence limits; time now to read the test.

The result

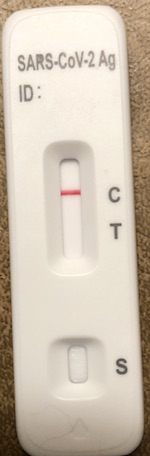Ultimately, as you can see here, the test was negative: only the C bar showed up (i.e., the test worked), and not a trace of the T bar (i.e., no viral antigens detected). Big sigh of relief! (Exactly 89.4% of the biggest possible sigh of relief, as you will understand if by some happy accident you chanced to wade through the math above.)

We also breathed sighs of relief on behalf of the elderly people visited this week by the Weekend Editrix and her minions. At least none of them will inadvertently get sick from the kindness of the Weekend Editrix, and her minions who visit them.

The Weekend Conclusion

1. In the US, our medical system in general is cruel, and our COVID-19 testing system is laughable: difficult of access and low availability to all if money were lacking.
2. People really don’t understand the difference between a False Positive Rate and a False Discovery Rate. Or appreciate that what they really want to know the Positive Predictive Value and the Negative Predictive Value. Tsk! (Admittedly, I have niche tastes.)
3. But after all that, we’re still relieved to be 89.4% sure we’re COVID-19 free here at Chez Weekend.

Addendum 2021-Dec-22: XKCD shows us all How It Is Done

A member of the Weekend Commentariat (email division) wishes to point out that Randall Munroe, the chaotic good genius behind the wonderfully perverse XKCD, has shown us all The Correct Way to interpret COVID-19 rapid antigen tests:

(Read the mouseover text. I want some of that anti-coronavirus COVID+19 stuff!)

---

Notes & References

1: JE Shuren, “Coronavirus (COVID-19) Update: FDA Authorizes Additional OTC Home Test to Increase Access to Rapid Testing for Consumers”, FDA.gov, 2021-Oct-04. ↩

2: ACON Laboratories Staff, “Flowflex COVID-19 Antigen Home Test Package Insert”, ACON Labs, retrieved 2021-Dec-10. ↩