The Weekend Retirement Portfolio

After reading my rant on the superiority of Treasury bonds vs corporate bonds as a stock diversifier, of course somebody asked me what the retirement portfolio of the denizens of Chez Weekend looked like. Basically: index funds, heavily diversified across bond types, stock sizes, valuations, and nations.

Getting Some Details Out of the Way

We have a small income from a pension, from a family business, and from the Weekend Editrix’s consulting work. It accounts for about 10% – 20% of our desired income. So the question is: how to structure our retirement portfolio so that, on a total return basis, we can withdraw enough each year to get the rest of our income.

We are deferring Social Security until I turn 70, as a way of maxing out its benefits as “longevity insurance”, i.e., it’s an inflation adjusted annuity we can’t outlive and can’t buy a replacement for anywhere else.

There’s a lot to unpack here: what’s a safe withdrawal rate, what’s a sensible asset allocation, and how much capital one needs at the start of retirement. The first 2 questions are for another time; here we’ll just estimate the capital requirement from simple high-school algebra.

Rick Ferri at the Bogleheads discussion board once suggested the following model (which I’ve cast into slightly more formal mathematical terms). Let:

\[\begin{align*} R &= \mbox{desired retirement income} \\ P &= \mbox{pension or annuity income} \\ S &= \mbox{anticipated Social Security income} \\ y &= \mbox{years until Social Security starts} \\ w &= \mbox{portfolio withdrawal rate} \\ C &= \mbox{investment capital available at start of retirement} \end{align*}\]

For the first $y$ years, you have pension income $P$ and have to supply $R - P$ income. Let’s conservatively assume that’s just a pile of cash in the amount $(R - P)y$ that you’ll spend over the next $y$ years.

Then after that, Social Security kicks in and you have income in the amount of $P + S$, so you have to supply $R - P - S$ income, i.e., the amount above pension and Social Security. That will come as a withdrawal at rate $w$ from a portfolio, so at that point the value of the portfolio must be above $(R - P - S) / w$. (NB: This does not address whether $w$ is a sustainable withdrawal rate!)

So the total capital required is the lump sum to spend before Social Security plus the portfolio from which to withrdraw after that:

\[C = (R - P) y + (R - P - S) / w\]

$P$, $S$, and $y$ are pretty much fixed by external circumstances. Thus we have a relationship between the retirement income $R$ and the withdrawal rate $w$. In practice, safe withdrawal rate studies show $3\% \le w \le 4\%$ is a relatively safe and reasonable place to be; that will tell you a range of achieveable incomes when you solve for $R$:

\[R = \frac{w C + S}{y w + 1} + P\]

It’s always worthwhile to check limiting cases! This equation behaves sensibly in a number of limiting cases:

• In the limit as $w \to 0$, income becomes just $R \to P + S$.
• In the limit as $y \to 0$, Social Security starts now and $R \to w C + P + S$.
• In the limit as $y \to +\infty$, Social Security never happens and the money has to last forever. So $R \to P$. (That’s because the capital $C$ doesn’t matter much spread across infinite years.)
• In the limit as $S \to 0$, then $R \to w C + P$, because we can then set $y = 0$ because there’s no point in waiting for a Social Security income of 0.
• In the limit as $C \to 0$, then $R \to P + S$ because if there’s no capital we might as well set the withdrawal rate $w = 0$ and start Social Security immeidately.

So that’s at least part of our framework for thinking about retirement income. Much of the rest is figuring out what a “safe” withdrawal rate means and what a sensible asset allocation is, in various mathematical ways. (Both of which are subjects for a later post.)

Asset Allocation: Ground Rules

A few ground rules:

• Use diversified mutual funds or ETFs, never try to pick stocks or bonds yourself.
• Always use index funds. Active management is of negative value.
• Use cheap index funds, i.e., low expense ratios. In the past this meant Vanguard, though there is some competition now. Vanguard is basically organized as a non-profit, unlike everybody else. I’ve been using Vanguard since about 1979 and like them.
• Use sensible asset classes: US total stock market index, foreign total stock market index, REIT index, Treasury/TIPS index of short-intermediate term, tilts to small and value stocks, and foreign bond index. ^[1]

Peter Bernstein wrote a famous article in 2002 about the virtues of a 60% stock / 40% bond portfolio. ^[2] While I won’t go so far as he did and recommend it to everybody all the time, it’s nonetheless what I probably want in early retirement.

We want to maintain international diversification too. The US is about 55% of the world stock market, so an unbiased portfolio would have a US/foreign ratio of 55/45. We achieve that partly through using VTWAX, the world stock index fund, equivalent to the ETF VT.

We also want to diversify across the value and size factors, so we include tilts in the stock portion to REITs (value-ish), US small value stocks, and foreign small stocks.

The Simplest Possible Portfolio

The simplest possible 60/40 portfolio, with global-neutral allocation, is actually possible:

• 60% VT (World Stock Index ETF)
• 40% BNDW (World Bond Index ETF)

True, BNDW contains corporate bonds and not just Treasuries. True, this portfolio doesn’t have small/value tilts. But… it’s just about as simple as possible! The only way to get simpler is with a single-fund investment in one of Vanguard’s funds of index funds, like VSMGX (Life Strategy Moderate Growth; not perfect about tax placement, but still pretty good!).

A Slightly More Complex Portfolio

We’re willing to tolerate a bit more complexity, though as I age the 1- or 2-fund versions above will no doubt get more attractive.

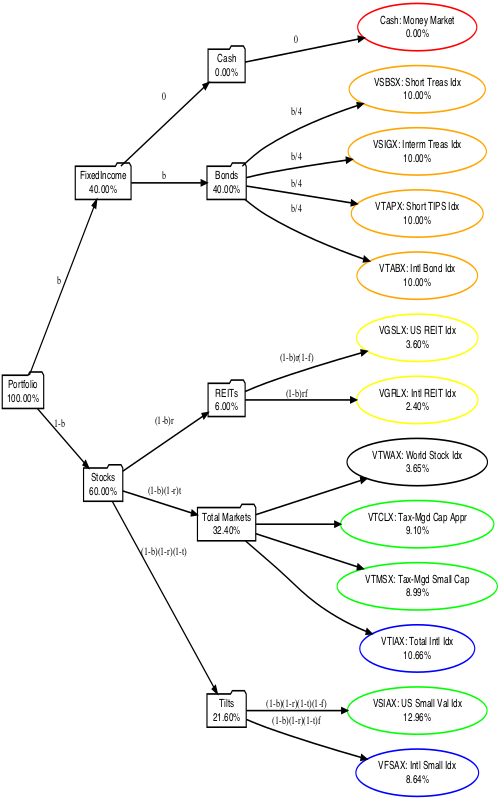Here’s a tree, showing how the asset allocation breaks down from left to right; the low risk investments are at the top, and the higher risk investments are at the bottom. The tree was drawn with an R script ^[3], available for peer review.

• The first split sets the stock/bond ratio at 60/40.
• Second, in bonds, we allocate 0% to cash and the 40% of bonds gets split equally between short term Treasuries, intermediate term Treasuries, short term inflation-protected TIPS, and foreign bonds.
• Third, in stocks, we split off 6% (or 10% of the 60% equity sleeve) into REITs, i.e., real estate. US tax law treats REITs in a funny way that makes them act a bit differently from regular stocks, so we want to capitalize on that. They are 60% US REITs and 40% foreign REITs.
• Fourth, we divide the remaining 54% devoted to equity into a total stock market index section and a tilt section.
  • The total stock market section would nominally be VTWAX, the world stock market index fund. But I have a bunch of legacy investments in a taxable account, more or less locked in by capital gains. Hence the presence of the other 3 funds; VTWAX is just used to fill out the rest of the total stock market allocation.
  • The tilts are to bias the portfolio toward value stocks and small stocks, since those have enhanced returns somewhat independent of the market in general according to the Nobel-winning Fama-French 3-factor model.

The summary rules for how to automate this are from 4 parameters $b$, $r$, $f$, and $t$, as labelled on the arcs in the tree:

• If $b = 0.4$ is the fraction to put in bonds, then $1 - b = 0.6$ is the amount in stocks.
• If $r = 0.1$ is the fraction of stocks to put in REITs, then $(1-b)r = 0.06$ goes in REITs. A fraction $(1-b)(1-r) = 0.54$ goes in the more broad stock indexes.
  • If $f = 0.4$ is the fraction of equity to put in foreign stocks, then US REITs get a fraction $(1-b)r(1-f)$.
  • Foreign REITs get $(1-b)rf$.
• If $t = 0.6$ is the amount to devote to total market indexing, so that’s $(1-b)(1-r)t = 0.324$.
• Then $1-t = 0.4$ then the amount to devote to small-value and small tilts is $(1-b)(1-r)(1-t) = 0.216$.
  • US small value gets $(1-b)(1-r)(1-t)(1-f)$.
  • Foreign small value gets $(1-b)(1-r)(1-t)f$.
• Avoid any transactions in the taxable assets, moving things in the IRAs instead.

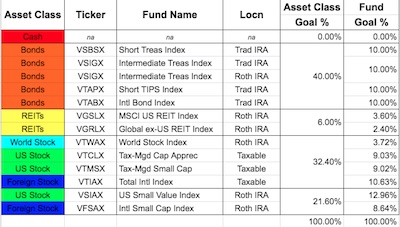
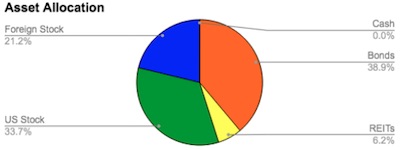
Here’s what it looks like in tabular form and in pie chart form. The colors code the same rising risk level with rising spectrum as in the tree. You can also see the tax placement here, i.e. whether it’s taxable, tax-deferred (Trad IRA), or tax-free (Roth IRA).

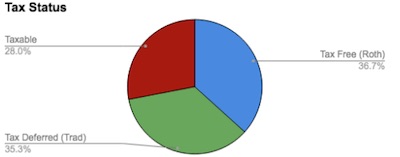Finally, here’s what we did for tax placement. We tried to have in taxable only stock funds that generate very little distributions (tax-managed, and foreign for the foreign tax credit). The Trad IRA is all bonds. The Roth IRA is everything else, i.e., stuff we hope grows a lot tax-free.

Each year we do a partial Roth conversion on the Trad IRA, to make sure that when the required minimum distriubtions start on the Trad IRA at age 72, they don’t cause a tax problem. Also, we take the political view that tax rates must go up in the US sooner or later, so we’d prefer to have assets in the Roth where they’re protected from that.

That’s… a little complicated. Even that’s not totally what we do; the Weekend Editrix has a small Roth IRA in a Vanguard Target Retirement fund of index funds, and I still have a (now very small) amount of my employer’s stock that I’m waiting to sell.

But this is pretty close.

The Weekend Conclusion

Basically, we have a portfolio of index funds designed to capture risk premiums where they’re available to a retail investor, not take dumb risks, and be as neutral as we can be about capitalization, valuation, and national location. We try to be reasonably tax-efficient.

It’s worked pretty well. As we age, we might simplify it down to a single fund like VSMGX (Life Strategy Moderate Growth), or even hire Vanguard Personal Advisory Services to do it for us.

---

Notes & References

1: Vanguard’s foreign bond index fund VTABX is currency-hedged back to the dollar, so it has no currency risk. It’s largely sovereign bonds of developed nations, so it looks like Treasuries. Vanguard always recommends it. The last time I looked, Vanguard’s evidence said it wouldn’t help diversification much… but wouldn’t hurt either. (See here, Figure 7 on p.10: note the broad, shallow “optimum” where the portfolio variance changes by only 0.2% as the foreign bond allocation goes from 0% to 100%!) So I decided to take Vanguard’s advice. ↩

2: PL Bernstein, “The 60/40 Solution”, Bloomberg Personal Finance, 2002-Jan-Feb. Retrieved via the Wayback Machine 2021-Jun-19.↩

3: Weekend Editor, R script to draw asset allocation tree, Some Weekend Reading blog, 2021-Jun-19. The data from a .tsv file describing the portfolio drives the graphics. There is also available, for peer review, a transcript of running the script. ↩