High $T_c$ Superconductors at Last?!

Last Saturday, 2022-Jun-22, two preprints from Korean physicists dropped on ar$\chi$iv. They claim room-temperature, ambient-pressure superconductivity in a chemically relatively non-exotic material. Let’s see what they’ve got.

Bearers of the News

Via Sabine Hossenfelder & Douglas Natelson came the news:

Ok, I confess: I had a few twinges from flashbacks to the 80s when the cold fusion via electrochemistry stuff came out. I wanted to believe, so hard. And it was painful to see the layers peeled back as Pons & Fleischmann were slowly flayed alive and exposed as having no clue.

Still… “This one looks potentially interesting.”

You can get conned if you’re too easily convinced; but nobody should want the boring life of refusing to hope good things are true. So let’s dive in and see if there’s reason to hope here.

A Tiny, Tiny Bit of Background on Superconductivity

This all gets more comprehensible both as physics and a potentially monumental achievement if you understand the background a little bit.

Ancient (20th Century) Prehistory: Type I and Type II Superconductors

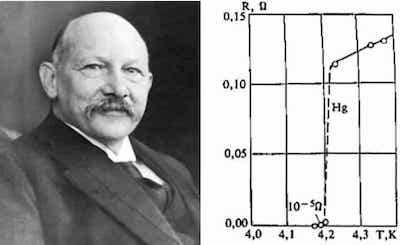The first superconductor discovered was in 1911, by Kamerlingh-Onnes looking at Hg in liquid He. At $T_c \sim 4.2\ \mbox{K}$, just a gnat’s whisker above absolute zero, the resistance went to 0 and all magnetic field was expelled. At various combinations of current and magnetic field, the new phase of matter “quenched” back to normal. It’s hard to overemphasize how weird this result was: currents sustained infinitely for no effort, sudden phase changes for no obvious reason, and even odder heat capacity results.

What Kamerlingh-Onnes was even thinking, doing resistance measurements on random metals at those extremely difficult to reach temperatures is beyond me. It always smelled a bit like doing plasma physics at the bottom of Death Valley. I mean, sure, you could do that… but why would you?!

Those were Type I superconductors: nice clean phase transition, well defined critical currents and magnetic fields, complete magnetic flux expulsion (Meissner Effect), usually pure metals, and absurdly low transition temperatures. Fascinating physics, but not much good from an engineering viewpoint.

Then in the 1930s came Type II superconductors: often a mix of materials, squishy phase transition, partial magnetic flux exclusion, higher $T_c$, forming vortex domains of superconductivity that became bulk superconductors because of how the domains linked up. Still fascinating, marginally useful because $T_c$ was so low it still required liquid He (expensive, as in “a Dewar full of liquid money”; also an increasingly rare, non-renewable resource).

Recent History: The Holy Grail

The Holy Grail was to get a superconductor with $T_c \ge 77\ K$, which is the boiling point of liquid nitrogen. LN2 is much, much cheaper to make (and renewable from, you know, air), so it’s much to be preferred over liquid He. If the transition temperature is comfortably higher than 77 K, then you can cool it down to 77 K with LN2 and then pump up the current & magnetic field.

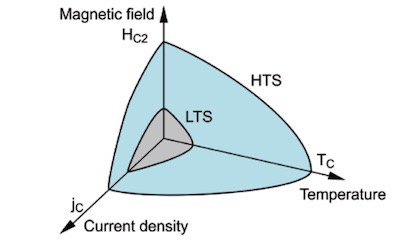There’s a really, really annoying constraint in superconductors: you can push either the temperature, the current, or the magnetic field, but not all 3. Sometimes not even any 2, as indicated schematically here by Figure 12 from a recent lightly-technical review by Bussmann-Holder & Keller. ^[1] If you try anyway, the superconductor quenches back to normal, and all the energy in the magnetic field (which scales like $B^2$!) is released.

(“All the energy released” is a very polite euphemism describing the explosion of a small to medium sized bomb. Bad idea. Trust me: I won’t tell you now I know that, but I do know exactly how bad an idea that is, failing to respect the energy density in a gnarly magnet.)

In the mid-1980s, people began looking at cuprate ceramics. Ceramics are brittle, and thus make miserable wires. As I recall Eric Drexler saying at the time, “If you hand people something that looks like a wire, the first thing they’ll try to do is wind it into a coil.” Ceramics were not really suitable for that.

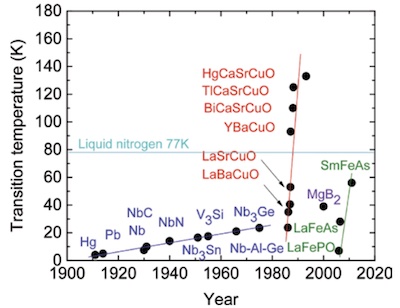But… one thing led to another and in 1987 Wu, et al. came up with an yttrium-barium-copper-oxide preparation with $T_c \gt 93\ \mbox{K}$. ^[2] That’s when the race started, as shown in this plot, also from Bussmann-Holder & Keller. NB: the near-vertical red line is the cuprate series, climbing very quickly starting in the late 1980s.

They all have some similarities: the copper oxides form layers, with other stuff sandwiched inbetween. Something about this is important. While we have a comprehensive theory of the mechanism of ordinary superconductivity (BCS theory, in 1957), we don’t have universal agreement on the high-$T_c$ sector. People have their favorites, for example the authors of today’s paper, q.v., favor something called 1-dimensional BR-BCS.

Back in the 80s, theoretical work on this was wild. People proposed anyons (particles that are neither bosons nor fermions because their 2-dimensional pseudoparticles and the spin-statistics theorem doesn’t quite fit), antiferromagnetic spin fluctuations, interlayer couplings, and so on. There’s still no universally (or even widely) accepted answer.

But, this all became practical. The superconducting magnets used in the tokamaks being built by Commonwealth Fusion Systems are REBCO (rare-earth barium copper oxide, the rare earth here being yttrium). Yttrium is problematic, as it’s hard to find (hence “rare”). Much of rare earth production is sourced from China, which instantly brings in political, trade, and potentially military problems that nobody wants.

CFS’s REBCO magnets have a demonstrated 20 T field strength and run a current of 40.47 kA, both quite impressive. Though the material has $T_c \sim 90\ K$, they will run at much lower temperatures (~ 20 K, if I recall correctly) to get some running room in critical field and critical current (see above).

So they still need liquid He for cooling. And we’ll see below why the new superconductors might not help, at least not initially (low critical current and low critical field). Perhaps later materials will be better.

Room Temperature (But Not Pressure)

Other people have found near-room-temperature superconductors, but in each case the transition required very high pressures that make them fascinating physics but never a likely engineering choice. (Except, of course, in science fiction stories about beings living at high pressures. Say, in the core of Jupiter under its crushing atmosphere.)

For example, in 2015 some hydrates of H${}_2$S reached a nicely high $T_c \sim 203\ K$, but only at 15,500 atmospheres. ^[3] This is easily achievable in the lab, even with a hand-cranked diamond anvil pressure cell. But it’s not going to happen for a power transmission line!

But that set off the search for other things that might superconduct at high temperatures, just at less insane pressures. Earlier this year a nitrogen-doped lutetium hydride showed a transition temperature of $T_c \sim 294\ K$ (“room” temperature is ~300 K)… but only at 10,000 atmospheres. ^[4] (Also: Lutetium… really? Ick.)

Better (higher temperature & lower pressure), but not enough better to matter.

Still: it set off some interest in high-pressure materials, either by shrinkage from cold or by brute-force pressure.

Last Week’s High-$T_c$, Ambient $P$ Superconductor Papers

Enough background!

Today’s papers causing all the excitement are a pair of preprints that dropped on arχiv last weekend. ^{[5] [6]} They’re from an overlapping group of Korean researchers at a couple Korean universities and research institutes (and one peculiar small company). Their funding appears to be from various Korean research grants.

The authors are Lee, Kim, and Kwon on the first paper, and Lee, Kim, another Kim, Im, and Auh on the second. There are so many authors on the second because they did X-ray diffraction (XRD), crystallography, X-ray photon spectroscopy (XPS), SQUID analysis, electron paramagnetic resonance spectroscopy (EPR), and, for all I can tell, a colonoscopy (because why not?). If you’re going to throw all that measurement tech at the problem (and in this case you should), then lots of your colleagues who are experts at those measurements will want on board. If anything, I’m surprised the author list is so short.

There’s something important to remember, as we read through these very rough papers, with spelling mistakes, misnumbered figures, oddly-drawn plots, mistakes with subscripts in chemical formulae, and all that. Namely: this is a very, very early report of a potentially important result. You should expect a certain amount of almost-but-not-quite amateurish stuff. This is not because anybody’s an amateur; it’s because they’re in a hurry. So start off by respecting that, and cutting them some slack on those kinds of issues.

My very favorite illustrative issue of this sort is the following string, which occurs a couple times in the 2nd paper:

오류! 책갈피가 정의되어 있지 않습니다.,오류! 책갈피가 정의되어 있지 않습니다.

According to Google Translate, confirmed by Korean colleagues who are too generous with their time when I ask silly questions, this means:

error! Bookmark is not defined, Error! No bookmarks are defined.

So apparently it’s their bibliography software barfing on an unresolved link.

Personally, I think it’s charming and should be left in the final copy. But that’s just me. :-)

Preparation of LK-99 and Some Properties

The material in question starts from a Pb apatite called Lanarkite, which is then doped with Cu atoms. The final result is $\mbox{Pb}_{10 - x}\mbox{Cu}_{x}(\mbox{PO}_{4})_{6}\mbox{O}$, for $0.9 \le x \le 1.1$.

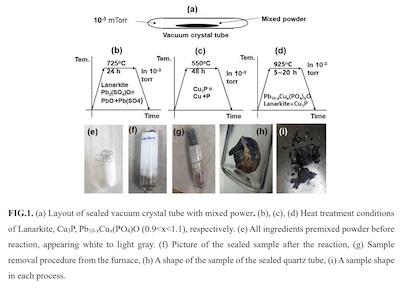The synthesis pipeline is shown in Fig 1a-i of the second paper, reproduced here.

• Synthesize Lanarkite by crushing in a mortar an equimolar mixture of lead oxide and lead sulfate, then bake at 725°C under $10^{-3}$ torr vacuum for 24hr:

  $\mbox{PbO} + \mbox{PbSO}_4 \rightarrow \mbox{Pb}_2(\mbox{SO}_4)\mbox{O}$.

  The result is a white powder.

• Prepare copper phosphide by mixing 3:1 molar ratios of Cu and P in a crucible (presumably carefully enough not to ignite the phosphorous, or under an oxygen-free atmosphere?). Then bake at 550°C for 48hr under $10^{-3}$ torr vacuum. The reaction will be:

  $3\mbox{Cu} + \mbox{P} \rightarrow \mbox{Cu}_3 \mbox{P}$.

• Mix the Lanarkite and copper phosphide in a crucible (what ratio?), and crush to powder. Bake at 925°C under $10^-3$ torr vacuum for 5-20hr. They don’t say exactly, but I expect the baking time will vary the amount $x$ of copper doping.

  The sulfur will evaporate in the oven, so handle that.

Honestly, the pictures look like boring old charcoal. But that just goes to show you how deceiving visual inspection is.

After all the XRD, XPS, EPR, SQUID (and probable colonoscopy), they conclude that their material is “polycrystalline”. Given the way they just baked it, this is no surprise. We should expect some resistance showing up between crystal domains, but no particular orientation sensitivity as the domains should be randomly oriented. And indeed they claim to see that, so there’s progress to be made by growing larger crystals somewhat less violently.

The crystallography is consistent with a lead-apatite crystal structure, with copper doping sites and a few $\mbox{Cu}_2\mbox{S}$ impurities. However, the XRD data say the crystal has been compressed in 2 dimensions, with cell lattice base vectors going from values in lead apatite of:

\[\left\{ \begin{align*} a &= 9.865 \ \mathring{\text{A}} \\ b &= 7.431 \ \mathring{\text{A}} \end{align*} \right.\]

compressed, very slightly by $0.003 - 0.022 \ \mathring{\text{A}}$, down to:

\[\left\{ \begin{align*} a &= 9.843 \ \mathring{\text{A}} \\ b &= 7.428 \ \mathring{\text{A}} \end{align*} \right.\]

It’s not a lot, but it’s enough to shrink the crystal volume by 0.48% by lead/copper substitution. This squeezing is apparently important: they have a theory that both cold temperatures and high pressure have squeezed lattices in the past where superconductivity is observed, so this is just a different way of building a squeezed crystal.

Well, maybe… let’s wait for experimental confirmation and then let the theorists weigh in on that.

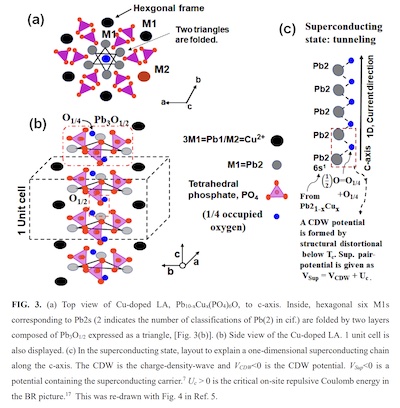In the meantime, they have a theory that the cuprate layers threaded together by Pb/Cu chains are part of the superconducting mechanism. They propose superconducting quantum wells (SQWs) in the cuprate layers, and that the squeezing effect makes it more likely for electrons to tunnel to the next layer via the Pb chains.

This is shown in Fig 3 of the second paper, reproduced here. I’m not competent to comment other than it’s an interesting alternative to conventional BCS. (“Interesting, if true”, as HL Mencken is supposed to have answered on the subject of UFOs.)

This, then, is the material they call LK-99. The 2 letters are the 2 (Latin alphabet) initials of the surnames of the primary authors. It may be this is their 99th attempt, or they may just think 9’s are cool. I note with some trepidation that in the second paper, LK-99 is now apparently trademarked, so the lawyers are already here.

Some thoughts:

• Somebody described it as like a car windshield of tempered glass, i.e., with stress literally baked into the material.
• It’s a plausible material, in that it extends the cuprate high-$T_c$ trend, and is relatively easy to make in polycrystalline form.
• But a more monocrystalline form may perform much better, though way more difficult to make?
• The volume shrinkage due to Cu doping may indeed substitute for pressure in the other examples of room temperature high-$T_c$ materials.
• Sometimes the ratios are a little unclear between the 2 papers. Crystal structure and words claim 1:4 Cu:Pb, chemical formula is 1:9 (depending on $x$), and preparation is 3:2. Ok, this will eventually get straightened out. And optimized.

The most interesting part is this is made of commonly available materials. There are no rare earths like yttrium in it. We do not require “unobtainium”, produced only in the country of Outer Explodistan with its notoriously touchy single-party government of the Neo-Marxist-Friedmanite Conservatives of the Old School, currently embroiled in a civil war over Structuralist vs Post-Modernist interpretations of the poetic works of Genghis Khan. By comparison, lead, sulfur, oxygen, phosphorous, and copper are pretty widespread to the point of near unavoidability.

On the other hand, lead?! Ick. If the optimized version of LK-99 still has lead, we’ll need very stringent regulation, tracking every gram of lead going into a factory and the superconductor & waste streams coming out. And there will have to be heavy criminal penalties for not recycling the lead-containing superconductors at end-of-life. I suggest something like the Sarbanes-Oxley law in the US, where corporate high executives are personally liable and subject to prison for violation.

The last time we trusted large companies (leaded gasoline) it didn’t work out at all well for anybody. ^[7] (← Read the footnote, Bunky!)

NB: The details of the recipe are slightly different between the 2 papers. The first paper says $x < 1.0$, while the second says 1.1. The second paper says the Lanarkite synthesis should be done under $10^{-3}$ torr vacuum, the first does not. This is either because they’re understandably fiddling with the recipe, or those parts were written by 2 people with different grasps on the details.

4 Boxes Ya Gotta Tick for Superconductors

To even start convincing people you have a superconductor, you have to show there is:

1. a critical temperature $T_c$ for the phase transition with zero resistivity below $T_c$,
2. a critical current $I_c$ above which the sample “quenches” back to normal,
3. a critical magnetic field $H_c$ above which it also quenches, and
4. an exclusion of magnetic flux from the sample, either partially (Type II) or fully (Type I), called the Meissner effect.

You have to do all 4 of those before people will even begin to take it seriously. There’s more after that, but that’s the ante to get into the game. So let’s count their chips!

Critical Temperature $T_c$ and Zero Resistivity

First, critical temperature and zero resistivity. Consider, as shown here, Figures 1a&b from the first paper:

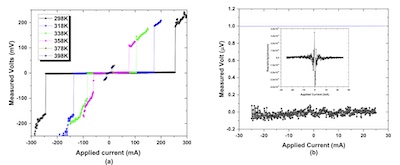
• Figure 1a shows what happened when:
  • They applied a fixed current across the sample, in both directions (+ and -) on the horizontal axis.
  • The vertical axis is the measured voltage drop across the sample, presumably due to resistance.
  • The colors encode various temperatures at which they did this.
    (The “fixed applied current” sometimes throws people since they’re used to thinking of applying a fixed voltage, not a fixed current power supply.)

  Consider the black line, at 298 K. There is 0 mV voltage drop across the sample, until the current reaches about 250 mA. This demonstrates both 0 resistance below some critical temperature $T_c \lt 298$ K, which we’ll get to below for critical current.

  As you can see, the same holds true as the temperature rises, but the window of current the sample will sustain with 0 mV voltage drop narrows down as we get closer to the putative $T_c$.

• Now consider Figure 1b. Here, there are 2 plots, the outer one and the inset one.
  • In the outer plot, they’ve zoomed in on the vertical axis by a factor of 1000, so we’re looking not at mV but at μV now. The horizontal axis is zoomed in by a factor of 10, so we’re looking at $\pm$ 30 mA instead of 300 mA.
  • In this zoomed-in view, most of the previous temperature samples are in the superconducting state. We expect to see 0 μV difference, and we pretty much do see that, with noise. You can argue about the mean and standard deviation differing from 0 μV, but that can wait for a later precision experiment. Crudely, the voltage across the sample at constant applied current is pretty much 0.
  • In the inset plot, they’ve calculated resistivity. Some of that involves sample size, which they did not report. But the main point is that this will sooner or later involve calculating $V/I$ for various values in the outer plot.
    • As long as you stay away from $I = 0$, the resistivity values are convincingly close to 0.
    • When you get close to $I = 0$, all hell breaks loose. You’re essentially trying to calculate numerically $V/I = 0/0$, where the numerator and denominator have mean 0 and some amount of noise. The result should jump around randomly, and indeed it does.
      
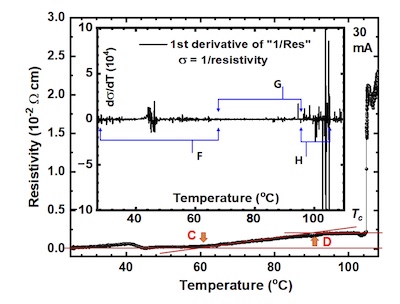
• Finally, consider Figure 5 from the second paper.
  • The outer plot is the more traditional resistivity $\rho$ versus temperature $T$ plot. (“Traditional” means it goes all the way back to Kamerlingh-Onnes, up at the top of this post.) Note that the horizontal coordinates are in °C, not °K!
  • The inner plot is the derivative of conductivity ($\sigma = 1/\rho$) with respect to temperature. This is proportional to something important called the density of states, i.e., the number of quantum states available to electrons at this temperature. Since it counts quantum states, it appears prominently in statistical mechanics where you look for the most probably quantum states. We’ll ignore it for now, even though the underlying physics is interesting.
  • The authors point out that the transition is a bit complicated:
    • Around 40°C something a little funky happens, with a bump of resistivity and the density of states doing something, but it then settles back down.
    • Around 60°C something happens, where there is a very slow (but small) rise in resistivity.
    • Around 90°C something else happens, and the resistivity flattens out, while the density of states goes nuts. (Probably related phenomena?)
    • Finally around 106°C = 379°K there is an abrupt rise in resistivity, indicating a transition to normal phase. Then the resistivity rises linearly, consonant with a metal using the Pb 6s2 band. (There’s a whole song and dance in the literature about whether high-$T_c$ superconductors use s-wave or d-wave electrons. Our authors today favor s-wave, for a variety of reasons in the paper which we’ll gloss over here.)

Conclusion: For a transition temperature $T_c$ below which $\rho = 0$, they’ve got pretty good evidence. Not perfect, and a bit unusually presented, but good enough to merit reproduction elsewhere.

Minor nit: they should report current density (current / unit cross-sectional area of sample). That’s the crucial thing, not total current. Still… enough to look further.

Critical Current $I_c$

As you’ll recall from the Bussmann-Holder & Keller plot above, there’s a constraint involving temperature, current, and magnetic field which bounds the superconducting state. We hinted at it above in Figure 1a of the first paper, but now let’s really consider their documentation for critical current $I_c$.

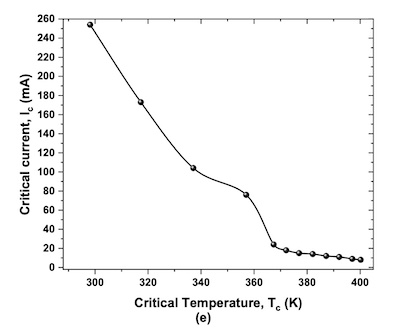
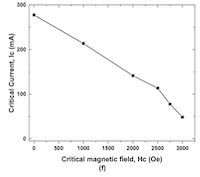
Figure 1e of the first paper, reproduced here, has the goods for us. They’re showing that as a function of temperature, there’s a maximum current $I_c$ that you can put through the sample.

Up around the critical temperature $T_c = 400$ K, you can barely put any current through it at all, maybe 10mA max. But down around 300 K, you can put about 250 mA through it.

This is exactly what we would expect of a superconductor, at least qualitatively. The shape of the curve is pretty funny, but given the polycrystalline nature of the sample, and probably multiple different isoforms in it or even impurities, this is not especially daunting. Perhaps a purer, more monocrystalline sample will look more as we expect?

Conclusion: For at least a qualitative sense of little current near $T_c$ and a lot more as you cool down, this makes pretty good evidence. Again not perfect, but probably the sample’s not perfect either, given how it was made.

Also note the critical current is small: 250 mA at room temperature. You’re not gonna transmit much power that way! (Recall the CFS magnets run about 40 kA, so $O(10^7)$ times more current.) Still… early days. The material may be optimized more, or may be a guide to discover better materials.

It’s a first step onto a big road.

Critical Magnetic Field $H_c$

As you’ll also recall from the Bussmann-Holder & Keller plot above, the constraint involving temperature, current, and magnetic field bounding the superconducting state implies a critical magnetic field $H_c$. Apply too much magnetic field, and the superconducting state shatters in your hand like a glass Christmas bauble, and goes normal.

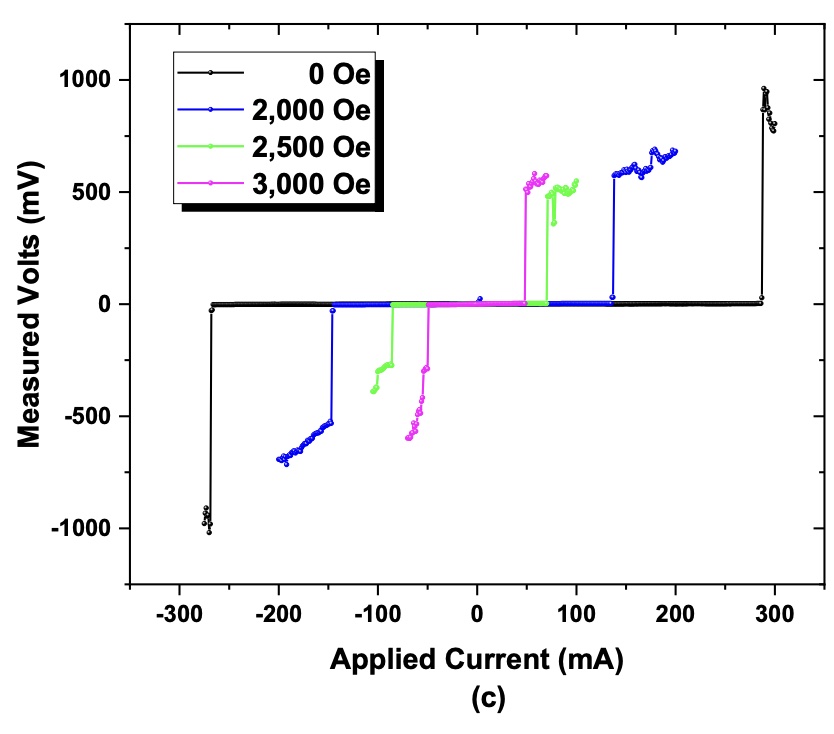
The evidence for that is shown in Figures 1c&f in the first paper.

• Figure 1c shows the by now familiar $V$ vs $I$ plot at some fixed unreported temperature, but now for various magnetic fields.
  • Note they’ve measured magnetic field in Oersteds, where 1 Tesla = 10,000 Oersteds. So the highest field considered here is 0.3 T, i.e., not terribly much by modern standards. (Recall the CFS fusion magnets are 20 T, so $O(10^2)$ more magnetic field.)
  • As you can see, at low magnetic fields (0.0 to 0.2 T) the range of applied current which keeps you in the superconducting state is around 250 mA in either direction.
  • But as you pack in the magnetic field, that comes down to maybe 50 mA either way.
  • This is what we expect to see.
• Figure 1f shows the same thing, in a different (more conventional) representation.
  • It shows the relation between the critical current $I_c$ and the critical magnetic field $H_c$.
  • As long as you stay in the lower left, you can be superconducting. If you cross into the upper right, you quench to the normal state (usually catastrophically).
  • Again, the exact shape of the curve is debatable, and not quite what I’d expect. But that can wait for confirmation and purer samples.

Conclusion: There is reasonable evidence for a critical magnetic field $H_c$. Some details look a little hinky, but at this stage with an early sample fabrication process, you’d expect that.

Meissner Effect: Flux Exclusion

Finally, the big guy: the Meissner effect.

Superconductors either partially (Type II) or fully (Type I) expel magnetic flux. So if you take a superconductor and put it in a magnetic field, it’ll repel that field, i.e., a strong diamagnetic effect.

Do we see that here?

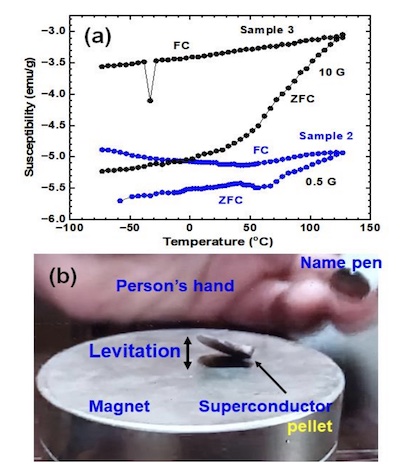The evidence is in Figure 4 of the second paper, reproduced here.

• Figure 4a is a bit complicated. It shows what happens when you cool a sample in the normal state, with and without magnetic field, down below the superconducting transition temperature.
  • In the normal state, samples allow magnetic field to penetrate them. They have a magnetic susceptibility (diamagnetic if $\chi \lt 0$, where the dipoles in the material align against the external magnetic field).
  • So when you cool them, the sample that initially contained a field will continue to do so, whereas the sample that did not contain a field will resist acquiring one. That’s what we see here, with $\chi \sim -3.6$ emu/g for the field-cooled sample but $\chi \sim -5.3$ emu/g for the zero-field-cooled sample.

• Figure 4b shows us this in a bit more graphic fashion. If you take a superconducting sample and put it on a big pole of a magnet, it will float. Here we see the sample partially floating, apparently because it’s big & heavy and the sample is not quite pure. But we can tell it’s room temperature & pressure because of the human hand in the background; never seen that before, given people’s understandable reluctance to put their hands in liquid helium!

  There’s a video of this available at ScienceCast/arχiv Video. Apologies for not being able to download or embed it, as would have been the case with YouTube! However, someone else had that same thought, and what’s shown here appears to be the same video, though labeled in Korean. The (automated?) voice-over is in English.

  This isn’t perfect:

  • They could have used a smaller sample that would have levitated; the dragging is a major sticking point here.
  • They clearly have samples of different purities (see curves in Figure 4a above). Is this one of the higher or lower purities?
  • Some other materials will also float, like certain paramagnetic forms of graphite.
  • Maybe pan the camera around so we can see the magnet details better; if it’s a single pole of a single magnet, this becomes more convincing!

Conclusion: I have a little bit of trepidation here, given that I only slightly understand the diamagnetic susceptibility argument in Figure 4a and the floating alleged to be the Meissner effect does not look perfect. So let’s score them a “low pass” on this one: partially convincing, but good enough to be worth looking at in another lab for reproduction.

Stuff That Looks a Bit Suspicious

Various people have proposed a number of things that look a little bit off, though nothing appears to be a showstopper. Here’s my (rebuttable) summary of some of those opinions:

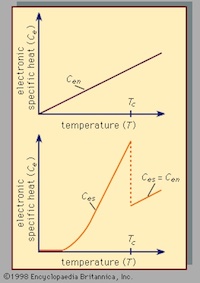
• Normally one measures the transition temperature with something called the Debye temperature, found on a plot of heat capacity vs temperature to find the phase transition, as shown in this image from Encyc Britannica. LKK claim that they shouldn’t do this because the usual (BCS) theories of superconductivity don’t apply to their SQW-tunneling-squeezed case. This is… a little bit suspect.

  They should measure it anyway, and let theorists explain the difference.

  But they’re experimentalists thrashing about for a theory, which often doesn’t end well. They just supply the recipe and the experimental results; others will reproduce the results (or not). Then theorists will start weighing in about mechanism. So LKK are trying to solve a problem they don’t have here – just measure the heat capacity vs temperature empirically and be done with it!

• They invoke the BR-BCS theory, instead of the conventional BCS, and invoke an analogy to Josephson junctions to explain their SQW tunneling. Others claim that BR-BCS doesn’t apply here; I’m not competent to have an opinion but note the disagreement.

  Again, this is experimentalists trying to invoke theory at too early a stage. Just show us the evidence, make us reproduce it, and the theorists will figure something out with you. This is not LKK’s problem, but they go on about it at length, anyway.

• Someone else – alas, I forget who! – doesn’t believe the magnetic susceptibility curves in Figure 4a above. There’s some kind of scaling problem where he thought a perfectly diamagnetic superconductor should have diamagnetism of -1, whereas this implies -154.

  Well, that’s serious. But I’m not competent (any more, alas) to find the discrepancy, let alone resolve it. Maybe somebody else can?

Problems With Superconducting Properties

So it really looks like a superconductor, modulo a few wrinkles, on all 4 aspects checked above. But before you start dreaming about super-magnets and lossless transmission lines, consider:

• Low critical field: $H_c \sim 0.3$ T, which is pretty low. The superconductor is “magnetically fragile” in that it goes normal in very moderate fields. Recall that the CFS tokamak magents, which are nitrogen-temperature (and lower) superconductors, run at 20 T. So you’re not making any big magnets with this material.
• Low critical current: $I_c \sim 250$ mA at 0 magnetic field. The superconductor is “current fragile” in that it goes normal at very moderate currents. Recall that the CFS tokamak magnets run at about 40 kA. So you’re not making any high-current applications, such as transmission lines, with this material.
• Not ductile enough: It looks more like brittle charcoal than anything else; you’re not going to form wires, let alone wind those wires into coils.

All of these are dismissible with the argument that this is the first try at finding a room-temperature, ambient pressure superconductor! Let’s just verify by reproduction at another lab that it works, then theorists will figure something out about mechanism, and we can proceed with optimization of the structure to be ductile, high-current, high-field, … and as wonderful as we imagine.

For example, the hypothesis of (a) squeeze cuprate layers that induce superconducting quantum wells and (b) layer-to-layer quantum tunnelling between layers along the lead (or other metal?!) vertical “rails” might be a good guideline.

Reproduction in Other Labs

Lest you think anybody’s dragging their feet, attempts to reproduce this result fly on apace. One group, amusingly named “MeissnerOrBust”, is livestreaming on Twitch, according to Sabine (who somehow – charmingly – seems to know everybody):

So we’ll see pretty soon! 2023-Jul-28 9:40pm US Pacific time is 2023-Jul-29 12:40am US Eastern Time.

The Weekend Conclusion

Whew! That was intense.

Some bottom-line thoughts:

• The material is $\mbox{Pb}_{10 - x}\mbox{Cu}_{x}(\mbox{PO}_{4})_{6}\mbox{O}$, for $0.9 \le x \le 1.1$, and there is a reasonably (not perfectly) specified recipe for making it.
• What’s the optimal values of $x$? “Optimal” in terms of $T_c$, $I_c$, and $H_c$ tradeoff.
• The oven method makes charcoal-ish polycrystaline stuff; can we do better with annealing the crystal domains, or something to remove inter-domain resistance as a problem?
• Oh, please, please, please: can we reproduce this with another metal besides Pb, so we don’t have to deal with the regulatory issues around toxicity? A common metal, not some exotic rare earth only available in Outer Explodistan, etc.?

• Can we make it ductile, to make something like a wire that we could wind into something like a coil?

  I mean, no criticism of LKK here. Good job discovering it at all. Enjoy your Nobel Prize. But charcoal is not wire, so there’s something for the next folks to do!

Even if we can’t make wires or coils, if we can add it to chips via molecular epitaxy or some such thing, we might be able to make superconducting quantum computing devices at room temperature. (Raw thought; I have explored literally no detail there.)

Conclusion: There are some problems, both of presentation and somewhat odd ways of showing the 4 points of superconductivity. But they all look more like rhetorical problems, not real physics problems. It’s very much worth the time of other labs to try to reproduce this!

Anybody wanna stay up & watch the video on Twitch reported above? Email me!

Addendum 2023-Jul-29: Life Gets Weird

Ok, now things are strange, which is how you know the story is real.

I tuned in to the livestream advertised above. Up until about 11:00pm EDT, it was a video of their oven with a countdown timer, and lots of peculiar spectators shooting strange emojis at each other in large quantity. Still… de gustibus, and all that.

I fell asleep, and woke up at 11:52pm EDIT, 12 minutes after the advertised start time. The channel was offline. Others had taken 30sec snaps showing the material being removed from the oven, then nothing.

Hmpf.

A couple others have claimed replication failure, but I have reservations. Overnight this went down:

• One was in Indian group who explicitly did not follow the preparation recipe, but tried something else (incorrect heating sequence, also probably got Cu doping wrong). Not really sure how that’s “replication”.
  

• Another was a press release only in Japanese text in an image shown here, with an alleged English translation. But the actual Japanese text just nonsense:

  On Sundays I eat roast chicken, sausage and pepperoni potatoes. LK99 I love ham & cheese lasagna, but it’s got high calories. Unless I eat junk food every week I gain excess calories and the chance of the diet getting delayed is 0%.

  Thanks, that was certainly… helpful.

• There was a similar fake non-replication “result” in Chinese, but with no names, no institutions, no procedural details, etc.

Well that’s weird.

In the meantime, somebody’s claiming the alleged problem with the magnetic susceptibility above was a graphical cut-and-paste error, which will be corrected. Ok, good, glad to hear it. Would prefer seeing it.

But then things got really weird: apparently there’s a schism among the authors.

1. Lee, the lead author, and a representative of Korea University gave interviews saying Kwon resigned or has been fired from both KU and the Q-Centre months ago, and published the first (3-author) paper without permission of the others, from reconstructed data.
   
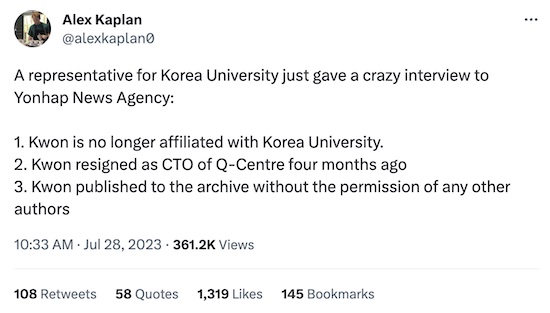
2. At the time of this interview, Kwon was actually presenting the results at a symposium, affiliating himself with both KU and Q-Centre! He also didn’t put the 2 main PI’s on the project on his title slide at all, which is usually a career-limiting move.
   
3. Lee says the 3-author paper posted by Kwon is retracted, and his 6-author paper without Kwon is the official one. But… Kwon apparently is on the patent they filed.
   

Something has gone really weird here. And not in the “good/interesting/fun” weird way. In the bad weird way. At least 1 person here is being a very bad actor, though at this point I can’t tell who that might be.

I’m gonna pay less attention to the drama, and more to the real replication attempts. Argonne is supposed to be on deck in a week or so. Maybe then we’ll know.

---

Notes & References

1: A Bussmann-Holder & H Keller, “High-temperature superconductors: underlying physics and applications”, Zeit. für Naturforsch., 2019-Jul-04. DOI: 10.1515/znb-2019-0103. ↩

2: MK Wu, et al., “Superconductivity at 93 K in a New Mixed-Phase Y-Ba-Cu-O Compound System at Ambient Pressure”, Phys Rev Lett 58:9, pp 908-910, 1987-Mar-02. DOI: doi:10.1103/PhysRevLett.58.908. ↩

3: AP Drozdov, et al., “Conventional superconductivity at 203 K at high pressures”, Nature 525:73, 2015. DOI: 10.48550/arXiv.1506.08190. ↩

4: N Dasenbrock-Gammon, et al., “Evidence of near-atmospheric superconductivity in a N-doped lutetium hydride”, Nature 615, pp. 244-250, 2023-Mar-08. DOI: 10.1038/s41586-023-05742-0. ↩

5: S Lee, J-H Kim, Y-W Kwon, “The First Room-Temperature Ambient-Pressure Superconductor”, arχiv, 2023-Jul-22. DOI: 10.48550/arXiv.2307.12008. Archived here for reference, since the posted copy will no doubt change with improvements/edits. ↩

6: S Lee, J-H Kim, H-T Kim, S Im, S An, KH Auh, “Superconductor $\mbox{Pb}_{10 - x}\mbox{Cu}_{x}(\mbox{PO}_{4})_{6}\mbox{O}$ showing levitation at room temperature and atmospheric pressure and mechanism”, arχiv, 2023-Jul-22. DOI: 10.48550/arXiv.2307.12037. Archived here for reference, since the posted copy will no doubt change with improvements/edits.↩

7: Interesting sidenote: both tetra-ethyl lead for gasoline and chloro-fluro-carbons (CFCs) for refrigeration were invented by Thomas Midgely Jr. The first caused horrible lead pollution and stunted a generation of inner city kids; the second came close to ecological disaster with ozone depletion before it was banned.

As far as I can tell, he was an ok guy… just incredibly unlucky. ↩