COVID-19: Paxlovid Rebound, or COVID-19 Rebound?

Is “paxlovid rebound” because of paxlovid, or because there are just a lot of COVID-19 rebounds?

On rebounds

Ok, I have to admit: I’m not entirely objective, here. I have a strong interest in not getting COVID-19 in general, as the last couple years of blogging here can attest. But given that I just had a case of COVID-19 (because of stupid crowding on MBTA buses with people who refused to mask), and got treated with paxlovid, I have a very strong Bayesian posterior interest in not getting paxlovid rebound.

So far, so good: RAT negative results, despite feeling a little off like a summer cold. Maybe it is a summer cold, for the first time in a couple years.

But it got me thinking: while there’s a lot of talk about “paxlovid rebound”, there’s always talk, because news reporters love “story” much more than they love truth.

Can we know the truth here? We need to know the rate of rebound among patients who get COVID-19 and are treated with paxlovid, vs those who get COVID-19 and are not so treated. Ideally, we’d like those 2 populations to be matched for age, complicating conditions, severity of infection, and everything else. (This being a non-ideal world, we will likely not get that.)

… and now, there’s data!

Remember: we want to compare rebound rates in paxlovid-treated and -untreated COVID-19 patient populations.

The untreated population

The first course in today’s Journal Club lunch is a medRχiv preprint by Deo, et al. ^[1] They looked at the untreated population, which creatively enough, turned out to be the placebo arm of another trial.

• $N$ = 567 patients total, so it’s of reasonable size, not some tiny little thing. (Though, frustratingly enough, we find later that only subsets were analyzed.)
• Anterior nasal swabs on days 0-14, 21, and 28.
• Daily scoring on 13 targeted symptoms every day, 0-28.
• Viral rebound defined as ≥ 0.5 log 10 viral RNA copies/mL increase above baseline. (Though, frustratingly enough again, they also use severe viral rebound thresholds of 3.0 and 5.0 log 10 mRNA copies/mL.)
• Symptom rebound by a 4-point total symptom score (i.e., likely a 5-point Liechert scale 0 - 4) increase above baseline.

I haven’t reviewed every detail here, since I’m not a referee. But overall, this looks like a very nice design: adequately powered, data collected on a dense time lattice, and end conditions pre-defined. Also, it doesn’t rely on case reports, which always have the threshold bias problem of whether physicians choose to report or not; here they started with a cohort and pursued every single person.

Results:

1. About 12% of patients had viral rebound, i.e., could test positive on a sensitive test. The rebounders were just a hair older, though just barely statistically significant ($p \sim 4\%$).
2. About 27% of patients had symptom rebound, i.e., reported feeling measurable levels of the 13 symptoms measured (like fever).
3. The combination of high-level viral rebound (≥ 5.0 log 10 RNA copies/mL) and symptom rebound was much rarer: 1% - 2%.

So some viral rebound above low threshold happens a lot. People also report feeling crappy for a while after COVID-19 (like your humble Weekend Editor). But, having both a high level of virus and major symptoms is pretty rare, though it does happen.

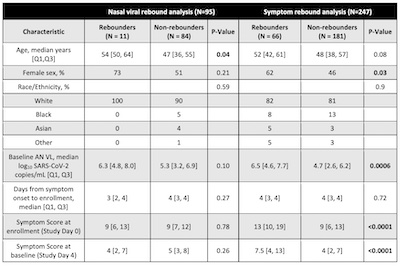Now, if you dig into the details a bit, you find that they didn’t analyze the whole cohort of 567 patients for each rebound criterion. (I didn’t dig into why.) Buried a bit at the end is Table 1, reproduced here, giving us the numbers.

• For viral rebound, they studied 95 cases = 11 rebounders + 84 nonrebounders.
• For symptom rebound, they studied 247 cases = 66 rebounders + 181 nonrebounders.

The authors did Mann-Whitney $U$ tests and Fisher Exact tests, so we’ll do something orthogonal and simple with a test of proportion: what’s the probability of rebound, and its 95% confidence interval?

> prop.test(11, 95)

	1-sample proportions test with continuity correction

data:  11 out of 95, null probability 0.5
X-squared = 54.568, df = 1, p-value = 1.501e-13
alternative hypothesis: true p is not equal to 0.5
95 percent confidence interval:
 0.06202404 0.20175069
sample estimates:
        p 
0.1157895 

> prop.test(66, 247)

	1-sample proportions test with continuity correction

data:  66 out of 247, null probability 0.5
X-squared = 52.615, df = 1, p-value = 4.057e-13
alternative hypothesis: true p is not equal to 0.5
95 percent confidence interval:
 0.2140326 0.3277695
sample estimates:
        p 
0.2672065 

As you can see, the rebound probabilities are consistent with what the authors report, though the confidence limits are larger than I’d thought, since they only analyzed a subset of the entire trial population:

• Viral rebound was at a chance of about 11.6% (CL: 6.2% - 20.2%).
• Symptom rebound was at a chance of about 26.7% (CL: 21.4% - 32.8%).

So far, so good.

Now, what about the patients who have both a high level of virus rebound (≥ 5.0 log 10 mRNA copies/mL) and a change in symptoms? That’s what we want to know about: a viral load high enough to be a spreader, and symptoms strong enough to make the patient miserable. We are, or should be, in the business of stopping disease spread and relieving misery!

The paper at this point dived into some complicated word salad that I didn’t feel like unmixing. They had multiple test cohorts, multiple symptom improvement/resolution criteria, multiple viral rebound thresholds, and not all patients had all viral or all symptom measurements (so there was presumably a database join operation that is not explained), and… look, I just got tired and decided to take their word for it.

The results are shown in Table 2, reproduced here.

Rather than undertake a deeper analysis here, let’s just note that the counts are very small: 0 - 4 patients out of cohorts of size 97 or 173, i.e., very rare. Rather than calculate so many different proportions and their confidence intervals, let’s just agree that they’re generally small and you can pick various numbers in 0% - 4%, with 2% as a middle of the road guess.

I appreciate that clinical practice is complicated, and people use multiple different criteria with multiple different thresholds. Sometimes they even have good reasons, beyond “that’s the way we do it at my hospital”. But sometimes not. The complexity is annoying, but it says we have a rebound probability of around 2%, and that it’s pretty rare just from the case counts.

Just for thoroughness, let’s take high-level viral rebound and symptom score rebound (2nd row in table 2) and the second cohort because it’s larger, with symptom rebound after improvement (3rd column in table 2):

> prop.test(2, 173)

	1-sample proportions test with continuity correction

data:  2 out of 173, null probability 0.5
X-squared = 163.14, df = 1, p-value < 2.2e-16
alternative hypothesis: true p is not equal to 0.5
95 percent confidence interval:
 0.002004929 0.045507333
sample estimates:
         p 
0.01156069 

So by those (somewhat arbitrary) criteria, the probability of a medically significant rebound and its 95% confidence limits are, for untreated patients, about 1.15% (CL: 0.20% - 4.55%).

The treated population

That’s what happens with untreated COVID-19: a rebound rate of 2%, give or take, depending on definitions of rebound measurements.

What about patients treated with paxlovid?

That’s the subject of a paper by Ranganath, et al. in Clinical Infectious Diseases. ^[2] While the paper is behind an execrable paywall, we can read the abstract and noodle around a bit to read what other people say after having read it. The top-line results are:

• 4 / 483 (0.8%) of patients had rebounds, by criteria not visible to me out here in front of the paywall.
• All 4 were vaccinated, and had mild symptoms treated with “additional COVID-19 therapy” which probably means more paxlovid.

> prop.test(4, 483)

	1-sample proportions test with continuity correction

data:  4 out of 483, null probability 0.5
X-squared = 465.17, df = 1, p-value < 2.2e-16
alternative hypothesis: true p is not equal to 0.5
95 percent confidence interval:
 0.002656212 0.022559795
sample estimates:
          p 
0.008281573 

So we should conclude the rate of COVID-19 rebound after paxlovid and its 95% confidence limit is about 0.83% (CL: 0.26% - 2.26%).

Comparison of treated vs untreated rebounds

Our topline results say, without treatment you’ve got about 1.15% chance of rebound, whereas with paxlovid you’ve got about 0.8% chance.

Is that difference statistically significant? You might guess “no”, given that their 95% confidence intervals more or less overlap. Indeed, that’s the case:

> prop.test(x = c(2, 4), n = c(173, 483))

	2-sample test for equality of proportions with continuity correction

data:  c(2, 4) out of c(173, 483)
X-squared = 1.3778e-30, df = 1, p-value = 1
alternative hypothesis: two.sided
95 percent confidence interval:
 -0.01786219  0.02442043
sample estimates:
     prop 1      prop 2 
0.011560694 0.008281573 

Warning message:
In prop.test(x = c(2, 4), n = c(173, 483)) :
  Chi-squared approximation may be incorrect

(The warning at the bottom is because there are so few rebound cases.)

But, basically the answer is no: the difference is not statistically significant. We should speak of “COVID-19 rebound”, not “paxlovid rebound”, because the rebound is a property of COVID-19, not the treatment by paxlovid. Rebounds happen. If you look for rebounds, you will find rebounds. But at not much difference in frequency with or without paxlovid.

(This is similar to claims I’ve heard about the paxlovid clinical trial: rebound cases were about the same in the treatment and control arms. The problem there is they looked only at maybe 2 time points, and at viral rebound only, not symptom rebound. So I haven’t looked into it personally, but the word on the street is consistent with what we observe here in these 2 studies.)

The Weekend Conclusion

It’s not paxlovid rebound, it’s COVID-19 rebound! Paxlovid has little to do with it.

It also seems amply clear that paxlovid should probably be prescribed for longer than 5 days, say 7-10 days to tamp down on the rebounds:

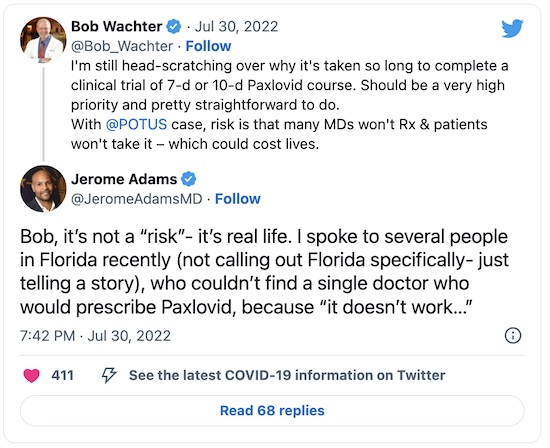
• That’s what the indispensable Bob Wachter of UCSF has been saying, loudly, for some time now.
• However, as the reply below from Jerome Adams indicates, we have even more severe problems pounding the facts into MD skulls about how well paxlovid works:

Maybe we need to make sure we’ve done at least some of the provider education needed to counteract disinformation and rumor, so providers will actually prescribe it, first.

Then we can update the guidance to recommend a second 5-day course in case of rebound, or just start with a 7-10 day course at the beginning. It’s not like paxlovid is in desperately short supply any more.

Ah, but will we actually do those things?

Glendower: I can call spirits from the vasty deep.

Hotspur: Why, so can I, or so can any man; But will they come when you do call for them?

— William Shakespeare, Henry IV Part 1, III:1, ll. 52-54.

Hotspur, despite his name, is the voice of admirably cool rationality here. Also, the pessimist.

Addendum, afternoon 2022-Aug-04: Self testing

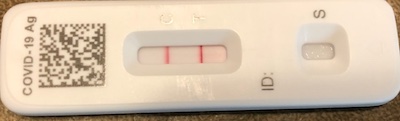After writing all this, I wondered if I should test again, given that I don’t feel great? I mean, what are the odds that the universe is that ironic?

As you can see here, the odds are excellent: it appears that your humble Weekend Editor is now the possessor of a case of COVID-19 rebound. Tired, achy, somewhat productive cough, runny nose, and about 1°C fever. So it’s mild, I guess?

At least I know it’s not paxlovid’s fault. It’s the damn virus!

Addendum 2022-Sep-16: A better result

See the comment below from Jonathan, who got the Raganath paper from behind the paywall. Comparing patients selected by similar criteria, rebound is 33x less likely with paxlovid than without! Rebound is definitely not paxlovid related, but rather COVID-related.

Even better.

Notes & References

1: R Deo, et al., “Viral and Symptom Rebound in Untreated COVID-19 Infection”, medRχiv, 2022-Aug-02. NB: At the time of writing, this is still a preprint, i.e., before peer review. ↩

2: N Ranganath, et al., “Rebound Phenomenon after Nirmatrelvir/Ritonavir Treatment of Coronavirus Disease-2019 in High-Risk Persons”, Clin Infect Dis, 2022-Jun-14. DOI: 10.1093/cid/ciac481.

NB: This is behind an execrable paywall. However, the abstract and other reliable sources ^[3] quote it as observing 4 / 483 (0.8%) of patients at high risk who got paxlovid later showed rebound symptoms at a median of 9 days after treatment. All 4 were vaccinated. The rebound cases were mild. They were treated with “additional COVID-19 therapy”, which we presume means additional paxlovid (though that’s not explicitly stated where I can see it).

Also, the FDA notes that in the clinical trial 1% - 2% of patients eventually had some evidence of rebound as measured by very sensitive PCR test, with or without symptoms. Importantly, this was true in both the treatment and placebo arms of the trial. ↩

3: P Wehrwein, “Paxlovid Rebound: Rare But Real”, Managed Healthcare Executive 32:6, 2022-Jun-14. ↩