On the Lifetime of Conspiracies

The world is full of conspiracy theories, more than I recall ever being the case in the past, before social media. How reasonable is it to expect that a conspiracy can (a) depend on secrecy, (b) involve a large number of people, and (c) survive for more than a couple years? Not very, according to a probabilistic model!

Anatomy of basic conspiracy failures

Intelligent people disdain “conspiracy theories”. But of course we all know there are conspiracies, since they’re exposed more or less constantly. Also, some conspiracies do not depend entirely on secrecy for their continued existence: we all know organized crime exists, but that does not stop it.

On the other hand, some conspiracy theories posit situations that depend on secrecy. For example, pharma companies can’t hold back a secret cure for cancer unless the secret is kept. Or the QAnon craziness about the government being run by a ring of pedophile cannibals depends on secrecy, because dead children have a way of marvelously focusing the attention of police.

So how long should we expect such a conspiracy to last? That’s the subject of a paper by DR Grimes of Oxford, published in PLoS ONE a couple years ago. ^[1] He assumes a conspiracy stays intact until someone reveals it. In this model, it’s always an insider snitch, never an outside investigator.

Let’s reconstruct his arguments.

First assume a few reasonable things about the attempts to reveal the conspiracy:

1. Each decision to reveal the conspiracy is an independent event.
2. The mean rate at which conspirators decide to reveal is constant.
3. No 2 acts of revealing occur at the same time.

We can model the arrival of reveal events as a Poisson distribution, if the revelations obey those conditions. The Poisson distribution tells us if we wait for time $t$, the probability distribution of the number of attempts $k$ to reveal the conspiracy will be:

\[\Pr(k | \lambda) = \frac{\lambda^k e^{-\lambda}}{k!}\]

where $\lambda$ is the mean number of times the conspiracy is revealed after an unspecified time. However, we’re more interested in the rate of revelations, not the mean number observed. So let $\lambda = \phi t$, where $\phi$ is the rate, i.e., mean revelation attempts per unit time. Then the probability mass function for the number of revelation attempts $k$ is:

\[\Pr(k | \phi, t) = \frac{(\phi t)^k e^{-\phi t}}{k!}\]

Now, we’re really interested in the first revelation only, since that one breaks the conspiracy. So the distribution of time until that event is essentially how long we can keep observing $k = 0$:

\[\Pr(k = 0 | \phi, t) = e^{-\phi t}\]

That’s the distribution of times over which we observe $k = 0$, no revelation of the conspiracy. We’re interested in the time until $k \gt 0$, i.e., when the conspiracy is revealed:

\[\Pr(\mbox{conspiracy lasts until $t$} | \phi) = 1 - e^{-\phi t}\]

That’s equation (1) of Grimes’s paper: the probability the conspiracy is revealed starts out at 0, and rises in an exponential fashion to 1 over time.

Next, how should we think about $\phi$? Clearly it should increase with the number $N$ of people involved, and with each conspirator’s probability of revelation per unit time $p$. We should also acknowledge that the number of conspirators can also be a strong function of time, i.e., $N = N(t)$. People die off, are killed off by co-conspirators, or their knowledge may become irrelevant over time.

Grimes proposes this in equation (2) of the paper:

\[\phi = 1 - (1-p)^{N(t)}\]

The 2nd term is the probability that all $N(t)$ people don’t reveal, so 1 minus that is the probability that at least 1 person reveals. That’s what we want.

Because $1-p$ is going to appear a lot, for convenience we denote $\psi = 1 - p$. So the relevant probability is now:

\[\Pr(\mbox{conspiracy lasts until $t$} | p, N(t)) = 1 - e^{-t(1 - \psi^{N(t)})}\]

This is equation (3) of the paper.

Correction for time-varying rates of exposure

There’s a correction posted on PLoS ONE a few months after the initial publication. ^[2] Though in this case, it looks to me a bit more like an extension than a correction: we’ve allowed $N(t)$ to be a function of time, but should also allow $p = p(t)$ and in general $\phi = \phi(t)$. This would be appropriate for a population that is inhomogeneous over time, e.g., subject to changing social attitudes about the conspiracy. So the products in the exponents should in general be integrals:

\[\begin{align*} \Pr(\mbox{conspiracy lasts until $t$} | p, N(t)) &= 1 - e^{-\int_0^t{dt' \phi(t')}} \\ &= 1 - e^{-\int_0^t{dt' (1 - \psi(t')^{N(t')})}} \end{align*}\]

A few more things have to be done numerically, rather than analytically. This also affects the cases below, where we vary $N(t)$ over time in various plausible ways. In those cases, it’s important to look at the figures in the correction, not the original paper. While one could also vary $p$ with time, we’ll follow Grimes’s example and keep $p$ (and hence $\psi$) constant.

Various ways to count who’s in on the conspiracy secret

Nobody says the number of people in on the secret is fixed. How might it reasonably vary?

1. Fixed $N$: Ok, maybe it doesn’t vary. There are some number of people in on it at the beginning, and they stay that way for the rest of eternity, all of them providing active coverup of the secret, for all time:

   \[N(t) = N_0\]

2. Conspirators die off naturally: In this case, the secret is kept more or less on its own, without requiring all conspirators to maintain it actively. As they die off, fewer of them are available to reveal the secret. In that case, the number of conspirators will usually obey the Gompertz distribution, widely used to estimate survival in things like life insurance:

   \[N(t) = N_0 e^{\frac{\alpha}{\beta}(1 - e^{\beta(t + t_e)})}\]

   where $t_e$ is the average age of conspirators at the start of the conspiracy and $\alpha$ and $\beta$ are Gompertz parameters to be estimated, typically about $\alpha = 10^{-4}$ and $\beta = 0.085$ for general human populations.

3. Conspirators are killed off or otherwise eliminated faster than naturally: As Benjamin Franklin is alleged to have printed in Poor Richard’s Almanac in 1735:

   Three may keep a secret if two are dead.

   If our conspirators take this to heart and begin murdering each other (or outside investigators pick them off, albeit without learning the secret), we may perhaps model $N(t)$ as an exponential decay:

   \[N(t) = N_0 e^{-\lambda t}\]

   This assumes the remaining conspirators do not revise their probability $p$ of revealing the conspiracy as they watch their fellows eliminated. This is unlikely to be true, e.g., as organized crime syndicate members watch their fellows go silently to jail; plea bargains exist for a reason!

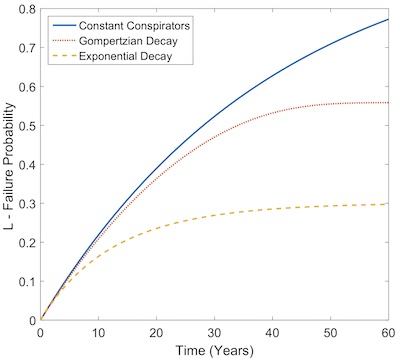The original paper shows a few intriguing graphs which have the probability of exposure peaking in a certain year in some of these models. However, once we apply the correction and use the integrals in the exponent, this feature goes away: the probability of exposure always increases with time, even if $N(t)$ decreases with time under the models above. Figure 1 in the correction shows us the situation, reproduced here.

• This shows the probability of exposure on the vertical axis and time in years since the start of the conspiracy on the horizontal axis.
• We assume an initial $N = 5000$ conspirators, each of whom has probability $p = 5 \times 10^{-6}$ of revealing the conspiracy each year.
• There are 3 different models of how $N(t)$ behaves over time:
  • In blue, the number of conspirators $N_0$ remains constant. This is clearly the worst case, as it maximizes the number of people who might reveal the secret!
  • The red dotted line in the middle is Gompertzian decay, i.e., conspirators dying off naturally. It assumes they’re mostly middle-aged ($t_e = 40$ years at the start).
  • The orange line shows a more murderous conspiracy, bent on keeping the secret by killing off their fellows so the number of conspirators is cut in half every 10 years.

Conclusion: For a reasonably complex conspiracy ($N = 5000$), the probability of being revealed is a near certainty in a few decades if all must keep the secret, better than 50-50 if they die off naturally, and still about 1/3 of the time if they keep the secret by systematically murdering each other. Keeping a secret in a large group is hard!

Calibration versus real-world events

Grimes went to some effort to calibrate his model against 3 well-known real-world conspiracies that were actually revealed, to see if the parameter fits made any sense:

1. The US National Security Agency’s PRISM scandal: It’s actually illegal for them to spy on US citizens inside the US. But they did it anyway, on the theory that their usually excellent operational security could keep it secret, and keeping illegality undiscovered was as good as being legal. It was exposed by Edward Snowden. (Hint: if the NSA’s opsec was not up to task here, why is your conspiracy likely to do any better?)
2. The US Public Health Service’s Tuskeegee syphilis experiment: From 1932 to about 1970, the US Public Health Service found a number of black men with syphilis, kept it secret from them, and withheld treatment “in order to study the disease”. This is one of the reasons, quite understandably, that American Blacks have a deep distrust of both government and the health care system. It was exposed by Peter Buxtun in 1972.
3. The US Federal Bureau of Investigation’s use of a number of pseudoscientific forensic tests: They used these dubious ‘tests’ to determine criminality in many cases without any basis in reality. Many were imprisoned for decades, and some even executed on the basis of these fraudulent tests. It was eventually exposed in 1998 by Frederic Whitehurst.

Without going into the detail available in the paper, all the conspiracies fit the model with some reasonable parameter settings. There are lots of ambiguities, such as deciding when the conspiracy started: in 1932 the Tuskeegee experiment may have been regarded as acceptable back then, whereas it is abominable today; what’s the “true” start date?

Other conspiracies examined: that the moon landing was a hoax, that climate change is a hoax, that vaccines cause autism or don’t work (recall this is 2016, before COVID-19), and that pharma companies are somehow holding back a cancer cure. They can all be fit as well, with various parameter settings that are at least not beyond the bounds of reason.

This holds even though Grimes chose parameter settings maximally favorable to conspirators!

Grimes’s grim conclusion

First, conspiracies are fragile:

The analysis here predicts that even with parameter estimates favourable to conspiratorial leanings that the conspiracies analysed tend rapidly towards collapse. Even if there was a concerted effort, the sheer number of people required for the sheer scale of hypothetical scientific deceptions would inextricably undermine these nascent conspiracies. For a conspiracy of even only a few thousand actors, intrinsic failure would arise within decades. For hundreds of thousands, such failure would be assured within less than half a decade.

This includes only internal failures; the efforts of outside investigation just make things worse for would-be conspirators.

Second, Grimes is also well aware of the backfire effect, when conspiracy-minded people presented with evidence like this may just dig in deeper:

The grim reality is that there appears to be a cohort so ideologically invested in a belief that for whom no reasoning will shift, their convictions impervious to the intrusions of reality. In these cases, it is highly unlikely that a simple mathematical demonstration of the untenability of their belief will change their view-point. However, for the less invested such an intervention might indeed prove useful.

So, yeah: we can change a few minds, but some minds are irreparably damaged and therefore unreachable. I have no good ideas for what to do about that.

Why we care

At some level, we care because we care about our society and the people who are its members: nobody should be deluded into taking stances detrimental to their own well-being and the well-being of all of us.

But we also care for a darker, and more dangerous reason: there is increasing violence directed against scientists. An article in PLoS Biology by Peter Hotez details some of this ^[3], as a warning to our community.

There is a troubling new expansion of antiscience aggression in the United States. It’s arising from far-right extremism, including some elected members of the US Congress and conservative news outlets that target prominent biological scientists fighting the COVID-19 pandemic.

When politicians call hysterically to cut off the salary of Tony Fauci, their base of “patriots” issues death threats. They feed into vaccine resistance, which kills people.

With absolutely no exaggeration whatsoever, this is beginning to resemble the repression of science under mid-20th century Fascism:

Historically, such regimes viewed scientists as enemies of the state. In his 1941 essay, Science in the Totalitarian State [10], Waldemar Kaempffert outlines details using the examples of Nazism under Hitler, Fascism under Mussolini, and Marxism and Leninism [10]. For example, under Stalin, the study of genetics and relativity physics were treated as dangerous western theories, and potentially in conflict with official social philosophies of state [11]. Today, there remain examples of authoritarian regimes that hold similar views. In 2019, the Hungarian Government under Prime Minister Viktor Orbán took over the control of the Hungarian Academy of Scientists. Brazil’s President Jair Bolsonaro cut funding for Brazilian scientific institutions and universities while downplaying the severity of the COVID-19 pandemic or undermining evidence of deforestation in the Amazon due to climate change.

This intimidation is deep and broad. For example, last February, Katelyn Jetelina (who blogs as Your Local Epidemiologist) had to “take a break” for security reasons. Death threats are not part of the bargain we took when we became scientists!

It’s become a grim, and increasingly dangerous time to be a scientist in the United States. Grimes concludes:

As Nobel Laureate and Holocaust survivor Elie Wiesel once pointed out, neutrality or silence favors the oppressor. We must take steps to protect our scientists and take swift and positive action to counter the growing wave of far-right antiscience aggression. Not taking action is a tacit endorsement, and a guarantee that the integrity and productivity of science in the United States will be eroded or lose ground.

The Weekend Conclusion

Conspiracy thinking is a danger to one’s self. It is a danger to society. As a scientist, it is now also a danger to me.

Conspiracies are fragile with respect to being disclosed, but can do unimaginable damage until then.

Fight them. Tooth and nail.

Addendum 2022-Jun-16: Criticisms & application to COVID-19 conspiracy theories

I had missed a couple things about this paper: (1) it came in for some harsh criticism, and (2) there’s a recent follow-up applying it to COVID-19.

Criticisms

Ok, the paper gets a fist in the face in lots of venues, but some of them are just comment sections in various places. So we won’t take those seriously. A couple showed promise:

• One that I thought would be worth taking seriously didn’t actually understand the model fitting: they thought the 3 examples (PRISM, Tuskeegee, and FBI forensics) were the only 3 data points available to fit a global model. The truth, of course, is that the model is re-fit to each new conspiracy theory, from an estimate of the number of conspirators required and a model of how they age. So nothing to see there, and I won’t bother linking to those critics.
• Another critic for which I had high hopes was published in a philosophy paper. They skipped over the math (never a good way to win my respect!) and claimed it had to “fail” on philosophical grounds… at which point they disappeared behind a paywall. I dislike paywalls already, and I’m most certainly not going to shell out on the hope that the rest is not just more drivel.

Application to the COVID-19 pandemic conspiracy theories

Now, on to the update, also by Grimes. ^[4] While much of our conspiracy-minded woes are self-inflicted, some are not, as Grimes points out (emphasis added):

Much of this is organic, arising from already existent conspiracy theories. An EU commission report, however, found ample evidence that Russian and Chinese state forces in particular had amplified and propagated conspiracy theories about COVID-19 [31], a finding echoed in American intelligence reports [32]. Such disinformation is typically spread with the aim of undermining societal cohesion in rival nations and sowing seeds of mistrust.

That’s more or less of a piece with the similar Russian disinformation that disrupted Hillary Clinton’s campaign, leading to the regrettable Trump years.

Here’s what Grimes promises, up front in the abstract (emphasis added):

In this article, an expanded model for a hypothetical en masse COVID conspiracy is derived. Analysis suggests that even under ideal circumstances for conspirators, commonly encountered conspiratorial claims are highly unlikely to endure, and would quickly be exposed.

Let’s see if he delivers on that.

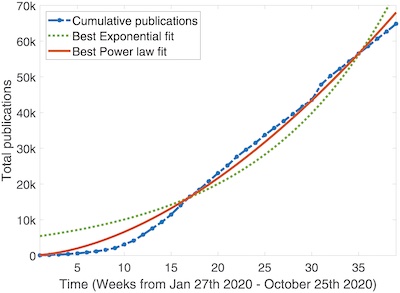All the models above from the original paper assume either a constant or shrinking pool of conspirators. Here, in order to sustain any of the florid delusions about COVID-19, we must accommodate a growing number of conspirators, as all the COVID-19 researchers must be in on the secret! So he models this by looking at the number of COVID-19 publications on a weekly basis, assuming a certain fraction of the authors are conspirators (he chose 3, as a conservative underestimate, i.e., favorable to keeping the secret). It turns out a power law fits this tolerably well (see Figure 2, reproduced here), with exponent and initial publication conspirators $\alpha = 1.714, r_0 = 383$. The number of conspirators would have to grow like:

\[N(t) = N_0 + r_0 (t - t_0)^\alpha\]

where $N_0$, the number of initial non-publication conspirators, is fit separately to each conspiracy theory, as they all have different requirements. But the model above for adding new conspirators as research progresses is the same for all of them.

This leads to a lovely mathematical model, involving lovely little monsters of the transcendental function world such as the exponential integral function. I haven’t re-derived it for myself, so I’m just going to trust the authors and the referees here.

He also uses a failure probability for each conspirator of $p = 7.69 \times 10^{-8}$/week, which is estimated from previous conspiracy models, scaled from per-year numbers down to per-week.

Some results:

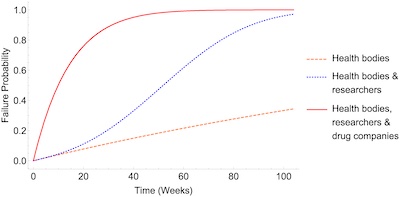
1. COVID-19 as a hoax or deliberately engineered pestilence: This requires a large nucleus of conspirators, starting with the public health agencies and progressively adding in researchers and drug companies. As shown in Figure 3, reproduced here, we see that the median failure time ranges from a bit over 170 weeks down to about 10 weeks, depending on how big the conspiracy is required to be.
   
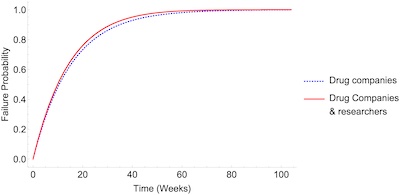
2. COVID-19 as a pretext for a nefarious mass vaccination program: This is a massive conspiracy, requiring at least the drug companies and possibly all the researches as well to be conspirators. (As a former drug company researcher at the beginning of the pandemic, I assure you nobody cut me a big check to keep quiet!) The result is shown in Figure 4, reproduced here. As you can see, the median time to failure is only about 10 weeks!
   
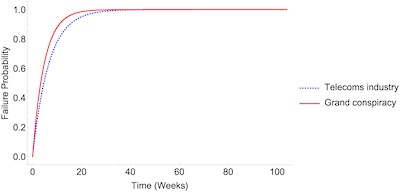
3. COVID-19 as a coverup for the hazards of 5G cell towers: This would require a truly “grand conspiracy”, as Grimes calls it, of most of the telecom industry, public health bodies, drug companies, and researchers. As shown in Figure 5, reproduced here, the mean time to failure is only 4 weeks!

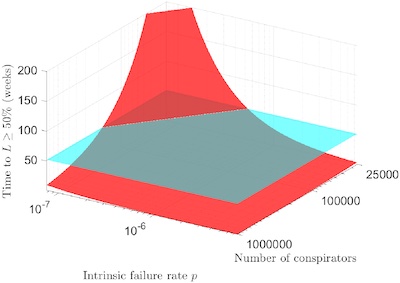The times to 50% chance of failure for the conspiracies of various sizes are all collected in Table 3 of the paper. Grimes estimated them from numerics on the model equations, not just eyeballing the graphs as we did here.

That’s summarized graphically in Figure 5, shown here, using model parameters outrageously generous to those favoring conspiracies (i.e., more realistic models would be exposed even sooner).

• The vertical axis is the time to 50% chance of exposure.
• The horizontal axes are the probability of leakage per conspirator per week, and the number of conspirators initially involved.
• The red surface shows how the time to exposure goes rapidly down as a function of both.
• The flat blue surface, for comparison, is at 1 year: about how long the pandemic had been going a the time this paper was published.

Basically, if your COVID-19 conspiracy needs to survive for more than 1 year, it had better be tiny and have very tight opsec to prevent leaks!

Conclusion: All the conspiracies tested, when inclusive of the realistic set of required conspirators, have a median failure time of 1 - 3 months. As we are now about 30 months into the pandemic (dating the start back to Nov/Dec 2019), those conspiracies are just about statistically impossible.

While this paper uncovers important truths, it remains to be seen if it will do us any good. Using the results of this paper would be employing expertise to debug people whose primary symptom is contempt for expertise. As Grimes points out, the problem is less a problem of expertise and more a problem of psychology:

Such refrains are unfortunately common in conspiratorial circles, with psychological studies consistently show a significant proportion motivated by an egotistical drive, and feeling of authority it induces [23, 60, 62]. With COVID-19, there is evidence that acceptance of conspiracy theory on the topic stems in part from a psychological disposition to reject information coming from experts and other authority figures [63]. Frequently this confidence in their beliefs is inversely proportional to their actual understanding. In one especially glaring example, anti-vaccine activists who proclaimed to know the most about vaccination and autism actually scored lowest in their knowledge of both subjects, despite rating their understanding as high [64]—a potent example of the Dunning-Kruger phenomenon [65], the observation that those least competent drastically overrate their understanding and ability. In many instances, the mere conviction that conspiracy theorists know more than others is especially intoxicating, and this motivation can be nigh on impossible to address [45].

So it’s frustrating, but the problem is real, and requires action:

Ultimately however, a serious conversation about how we address the dominance of medico-scientific conspiracy theories is urgently required. The COVID-19 crisis has laid bare the weaknesses in our system, and our inability to respond robustly to disinformation. Emerging evidence suggests that we can be immunised against certain forms of falsehood, provided this intervention comes before exposure [66]. Such an endeavour demands we embrace information hygiene as a society [56], encouraging people to treat all information as potentially pathogenic before they accept or propagate it. The potentially negative influence of social media companies on public understanding of science and medicine demands immediate investigation and further research too
[56]. In the interim, it is vital that physicians and scientists begin to address the odious influence of disinformation, before it undermines the vast strides we have made in the centuries since the enlightenment. Our future well-being is dependent upon it.

Here at Chez Weekend, we agree.

Even the Weekend Publisher, shown here, has instructed me to inform the world that he has purred in the general direction of this sentiment. (No, I don’t know how he knows the general direction of a sentiment. He’s a cat; inscrutability is part of the deal.)

---

Notes & References

1: DR Grimes, “On the Viability of Conspiratorial Beliefs”, PLoS ONE 11:1, e0147905, 2016-Jan-26. DOI: 10.1371/journal.pone.0147905. ↩

2: DR Grimes, “Correction: On the Viability of Conspiratorial Beliefs”, PLoS ONE 11:3, e0151003, 2016-Mar-01. DOI: 10.1371/journal.pone.0151003. ↩

3: PJ Hotez, “Mounting antiscience aggression in the United States”, PLoS Biology 19:7, e3001369. DOI: 10.1371/journal.pbio.3001369. ↩

4: DR Grimes, “Medical disinformation and the unviable nature of COVID-19 conspiracy theories”, PLoS ONE 16:3, e0245900, 2021-Mar-12. DOI: 10.1371/journal.pone.0245900. ↩